题目内容
用反证法证明命题:“a,b∈N,ab可被5整除,那么a,b中至少有一个能被5整除”时,假设的内容应为( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b不都能被5整除 | D.a不能被5整除 |
B
解析试题分析:解:由于反证法是命题的否定的一个运用,故用反证法证明命题时,可以设其否定成立进行推证.命题“a,b∈N,如果ab可被5整除,那么a,b至少有1个能被5整除.”的否定是“a,b都不能被5整除”.故应选B.
考点:反证法
点评:反证法是命题的否定的一个重要运用,用反证法证明问题大大拓展了解决证明问题的技巧

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将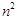 个正整数
个正整数 、
、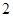 、
、 、…、
、…、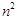 (
(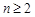 )任意排成
)任意排成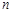 行
行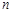 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数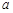 、
、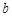 (
(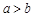 )的比值
)的比值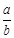 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当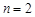 时, 数表的所有可能的“特征值”最大值为
时, 数表的所有可能的“特征值”最大值为
A. | B.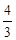 | C.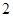 | D.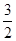 |
用反证法证明命题:若整系数一元二次方程 有有理数根,那么
有有理数根,那么 中至少有一个是偶数,下列假设中正确的是 ( )
中至少有一个是偶数,下列假设中正确的是 ( )
A.假设 都是偶数 都是偶数 | B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个偶数 至多有一个偶数 | D.假设 至多有两个偶数 至多有两个偶数 |
用反证法证明命题“设a,b∈R,|a|+|b|<1,a2-4b≥0,那么x2+ax+b=0的两根的绝对值都小于1”时,应假设
| A.方程x2+ax+b=0的两根的绝对值存在一个小于1 |
| B.方程x2+ax+b=0的两根的绝对值至少有一个大于等于1 |
| C.方程x2+ax+b=0没有实数根 |
| D.方程x2+ax+b=0的两根的绝对值都不小于1 |
用反证法证明“如果a>b,那么 >
> ”假设的内容应是( )
”假设的内容应是( )
A. = = | B. < < |
C. = = 且 且 < < | D. = = 或 或 < < |
下列推理是归纳推理的是( ).
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜出椭圆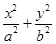 =1的面积S=πab =1的面积S=πab |
| D.科学家利用鱼的沉浮原理制造潜艇 |
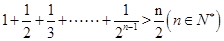 ,第二步由k到k+1时不等式左边需增加( )
,第二步由k到k+1时不等式左边需增加( )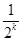
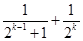
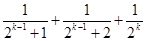
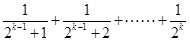
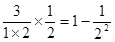 ; ?
; ? ;
; ,
, 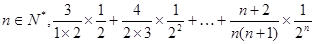 = .
= .