题目内容
下列推理合理的是( )
A.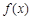 是增函数,则 是增函数,则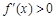 |
B.因为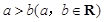 ,则 ,则 |
C.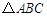 为锐角三角形,则 为锐角三角形,则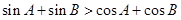 |
D.直线 ,则 ,则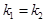 |
C
解析试题分析:根据题意,由于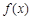 是增函数,则
是增函数,则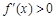 或者f’(x)=0在个别点成立,故错误对于B,因为
或者f’(x)=0在个别点成立,故错误对于B,因为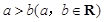 ,则
,则 显然不成立,对于D直线
显然不成立,对于D直线 ,则
,则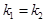 ,可能斜率都不存在,故错误,故选C.
,可能斜率都不存在,故错误,故选C.
考点:推理与证明
点评:主要是考查了合情推理的运用,属于基础题。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a8+b8=( )
| A.28 | B.47 | C.76 | D.123 |
用反证法证明“若a,b,c<3,则a,b,c中至少有一个小于1”时,“假设”应为
| A.假设a,b,c至少有一个大于1 | B.假设a,b,c都大于1 |
| C.假设a,b,c至少有两个大于1 | D.假设a,b,c都不小于1 |
将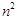 个正整数
个正整数 、
、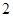 、
、 、…、
、…、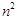 (
(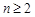 )任意排成
)任意排成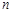 行
行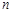 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数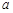 、
、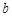 (
(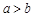 )的比值
)的比值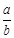 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当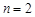 时, 数表的所有可能的“特征值”最大值为
时, 数表的所有可能的“特征值”最大值为
A. | B.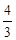 | C.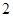 | D.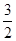 |
(推理)三角形的内角和为180º,凸四边形内角和为360º,那么凸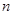 边形的内角和为
边形的内角和为
A.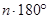 | B.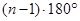 | C.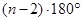 | D.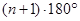 |
用反证法证明命题:若整系数一元二次方程 有有理数根,那么
有有理数根,那么 中至少有一个是偶数,下列假设中正确的是 ( )
中至少有一个是偶数,下列假设中正确的是 ( )
A.假设 都是偶数 都是偶数 | B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个偶数 至多有一个偶数 | D.假设 至多有两个偶数 至多有两个偶数 |
用反证法证明命题“设a,b∈R,|a|+|b|<1,a2-4b≥0,那么x2+ax+b=0的两根的绝对值都小于1”时,应假设
| A.方程x2+ax+b=0的两根的绝对值存在一个小于1 |
| B.方程x2+ax+b=0的两根的绝对值至少有一个大于等于1 |
| C.方程x2+ax+b=0没有实数根 |
| D.方程x2+ax+b=0的两根的绝对值都不小于1 |
用数学归纳法证明不等式1+ +
+ +…+
+…+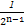 >
>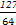 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
| A.7 | B.8 | C.9 | D.10 |