题目内容
13.已知a,b∈R+.(1)求证:$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{a}$≥a+b;
(2)利用(1)的结论,求函数y=$\frac{{{{(1-x)}^2}}}{x}+\frac{x^2}{1-x}$(0<x<1)的最小值.
分析 (1)利用综合法,通过证明a3+b3-a2b-ab2≥0,然后变形证明结果即可.
(2)利用(1)的结论直接求出最小值即可.
解答 (1)证明:a3+b3-a2b-ab2=a2(a-b)+b2(b-a)=(a-b)(a2-b2)=(a-b)2(a+b),
∵a,b∈R+.
∴(a-b)2(a+b)≥0,
即a3+b3-a2b-ab2≥0,
可得a3+b3≥a2b+ab2,
∴$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{a}$≥a+b;
(2)解:由(1)可得0<x<1时,函数y=$\frac{{{{(1-x)}^2}}}{x}+\frac{x^2}{1-x}$≥x+1-x=1.
函数的最小值为1.
点评 本题考查不等式的证明综合法的应用,函数的最值的求法,考查分析问题解决问题的能力.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
4.在平面直角坐标系中,过动点P分别作圆C1:x2+y2-4x-6y+9=0与圆C2:x2+y2+2x+2y+1=0的切线PA与PB(A,B为切点),若|PA|=|PB|若O为原点,则|OP|的最小值为( )
| A. | 2 | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\sqrt{5}$ |
1.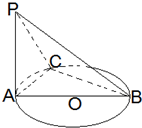 如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
 如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )
如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中互相垂直的平面共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
8.已知A=B={(x,y)|x∈R,y∈R },从A到B的映射f:(x,y)→(x+y,xy),A中元素(m,n)与B中元素(4,-5)对应,则此元素为( )
| A. | (5,-1)或(-1,5) | B. | (1,5)或(5,1) | C. | (-1,-20)或(-20,-1) | D. | (-1,-20) |
3.下列函数中,在(0,+∞)上为增函数的是( )
| A. | y=$\sqrt{x+1}$ | B. | y=(x-2)2 | C. | y=3-x | D. | y=log0.1(x+1) |