题目内容
若直线l：kx-y+2k-1=0与圆C：x2+y2+4x=0交于不同的两点A、B，则
•
的范围是 ．
| AB |
| AC |
考点：平面向量数量积的运算
专题：计算题,作图题,平面向量及应用
分析：由题意作图如右图，直线l：kx-y+2k-1=0恒过点（-2，-1）；C（-2，0），半径长为2；化
•
=（
+
）•
=4-
•
，从而由数量积的定义求解．
| AB |
| AC |
| AC |
| CB |
| AC |
| CB |
| CA |
解答：
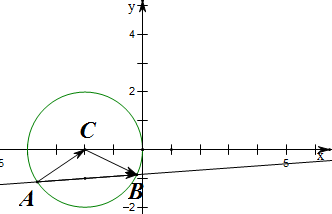解：由题意作图如右图，
直线l：kx-y+2k-1=0恒过点（-2，-1）；C（-2，0），半径长为2；
•
=（
+
）•
=
•
+
•
=4-
•
；
由图可知，120°≤＜
•
＞≤180°，
故4-
•
=4-4cos＜
•
＞；
∵-1≤cos＜
•
＞≤-
，
∴6≤4-4cos＜
•
＞≤8；
故答案为：[6，8]．
解：由题意作图如右图，直线l：kx-y+2k-1=0恒过点（-2，-1）；C（-2，0），半径长为2；
| AB |
| AC |
| AC |
| CB |
| AC |
=
| AC |
| AC |
| CB |
| AC |
=4-
| CB |
| CA |
由图可知，120°≤＜
| CB |
| CA |
故4-
| CB |
| CA |
=4-4cos＜
| CB |
| CA |
∵-1≤cos＜
| CB |
| CA |
| 1 |
| 2 |
∴6≤4-4cos＜
| CB |
| CA |
故答案为：[6，8]．
点评：本题考查了平面向量在几何中的应用，注意直线与圆所在的位置及特征是解决此题的关键．
练习册系列答案
相关题目
已知
=(a1，b1，c1)，
=(a2，b2，c2），则AB∥CD是
=
=
的（ ）
| AB |
| CD |
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |