题目内容
集合A={x|
}，B={x||x-b|＜a}，若a=1是A∩B≠∅的充分条件，则b的取值范围可以是（ ）A．-2≤b＜0
B．0＜b≤2
C．-3＜b＜-1
D．-2＜b＜2
【答案】分析：先化简A，B利用a=1是A∩B≠∅的充分条件确定b的取值范围．
解答：解：A={x|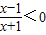
}={x|-1＜x＜1}，因为A∩B≠∅，所以a＞0，
则由B={x||x-b|＜a}，得B={x|b-a＜x＜b+a}，
当a=1时，B={x|b-1＜x＜b+1}，要使A∩B≠∅，
则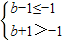
或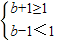
，
解得0≤b＜2或-2＜b≤0．即-2＜b＜2．
故选D．
点评：本题主要考查分式不等式和绝对值不等式的解法以及充分条件和必要条件的应用，比较基础．
解答：解：A={x|
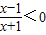}={x|-1＜x＜1}，因为A∩B≠∅，所以a＞0，则由B={x||x-b|＜a}，得B={x|b-a＜x＜b+a}，
当a=1时，B={x|b-1＜x＜b+1}，要使A∩B≠∅，
则
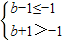或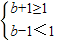，解得0≤b＜2或-2＜b≤0．即-2＜b＜2．
故选D．
点评：本题主要考查分式不等式和绝对值不等式的解法以及充分条件和必要条件的应用，比较基础．
练习册系列答案
相关题目