题目内容

10．已知圆的参数方程为$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.$（θ∈[0，2π]，θ为参数），将圆上所有点的横坐标伸长到原来的$\sqrt{3}$倍，纵坐标不变得到曲线C1；以坐标原点为极点，以x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为$ρsin（{θ+\frac{π}{4}}）=4\sqrt{2}$．
（Ⅰ）求曲线C1的普通方程与曲线C2的直角坐标方程
（Ⅱ）设P为曲线C1上的动点，求点 P与曲线C2上点的距离的最小值，并求此时P点的坐标．

分析 （Ⅰ）由已知可得曲线C1的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$，消去参数θ可得，由三角函数公式可化极坐标方程为ρcosθ+ρsinθ=8，可得x+y=8；
（Ⅱ）由题意可得距离d=$\frac{|\sqrt{3}cosθ+sinθ-8|}{\sqrt{2}}$=$\frac{|2sin（θ+\frac{π}{3}）-8|}{\sqrt{2}}$，由三角函数的最值可得．

解答 解：（Ⅰ）由已知可得曲线C1的参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$，
消去参数θ可得$\frac{{x}^{2}}{3}$+y2=1，
∵曲线C2的极坐标方程为$ρsin（{θ+\frac{π}{4}}）=4\sqrt{2}$，
∴ρcosθ+ρsinθ=8，即x+y=8；
（Ⅱ）设P（$\sqrt{3}$cosθ，sinθ）为曲线C1上的动点，
则点P与曲线C2：x+y=8上点的距离d=$\frac{|\sqrt{3}cosθ+sinθ-8|}{\sqrt{2}}$=$\frac{|2sin（θ+\frac{π}{3}）-8|}{\sqrt{2}}$，
当sin（θ+$\frac{π}{3}$）=1即θ=$\frac{π}{6}$时，d取最小值3$\sqrt{2}$，此时P（$\frac{3}{2}$，$\frac{1}{2}$）

点评 本题考查参数方程和极坐标方程，涉及三角函数的最值，属基础题．

练习册系列答案
相关题目
15．已知圆C：x2+y2+2x-4y+m=0与y轴相切．
（1）求m的值；
（1）若圆C的切线在x轴和y轴上的截距相等，求该切线的方程；
（2）从圆C外一点P（x，y）向圆引切线，M为切点，O为坐标原点，且有|PM|=|PO|，求使|PM|最小的点P的坐标．
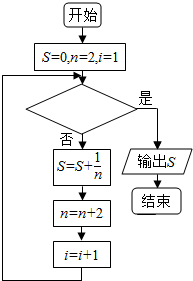1．如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{100}$的值的一个程序框图，其中判断框内应填入的条件是（　　）
A．i≥49？B．i≥50？C．i≥51？D．i≥100？
18．已知p：（$\frac{x-4}{3}$）2≤4，q：x2-2x+1-m2≤0（m＞0），若￢p是￢q的必要非充分条件，求实数m的取值范围．
5．已知$|{\vec a}|=1$，$|{\vec b}|=2$，$\vec a$与$\vec b$的夹角为$\frac{π}{3}$，那么$|{4\vec a-\vec b}|$等于（　　）
A．2B．6C．$2\sqrt{3}$D．12
15．若$\overrightarrow{a}$=（2+λ，1），$\overrightarrow{b}$=（3，λ），若＜$\overrightarrow{a}$，$\overrightarrow{b}$＞为钝角，则实数λ的取值范围是$λ＜-\frac{3}{2}$且λ≠-3．
2．求下列各式的值：
（1）若$\frac{π}{2}$＜α＜π，且sinα=$\frac{4}{5}$，求$\frac{sin（2π-α）tan（π+α）cos（-π+α）}{sin（\frac{π}{2}-α）cos（\frac{π}{2}+α）}$的值，
（2）lg200+$\frac{1}{2}$lg25+5（lg2+lg5）3-（$\frac{1}{27}$）${\;}^{\frac{1}{3}}$．
19．已知函数f（x）=x2+|x-a|．
（1）当a=1时，求函数f（x）的最小值；
（2）试讨论函数f（x）的奇偶性，并说明理由．
20．设命题p：函数f（x）=x3在R上为增函数；命题q：函数f（x）=sin（$\frac{π}{2}$+x）为奇函数，则下列命题中真命题是（　　）
A．p∧qB．p∧（￢q）C．（￢p）∧（￢q）D．（￢p）∨q

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网