题目内容

20．已知函数f（x）=2x，x∈[0，3]，则g（x）=f（2x）-f（x+2）的定义域为[0，1]．

分析 根据复合函数定义域之间的关系进行求解即可．

解答 解：∵f（x）中x的取值范围是[0，3]，
∴$\left\{\begin{array}{l}{0≤2x≤3}\\{0≤x+2≤3}\end{array}\right.$，得$\left\{\begin{array}{l}{0≤x≤\frac{3}{2}}\\{-2≤x≤1}\end{array}\right.$，
得0≤x≤1，
即函数的定义域为[0，1]，
故答案为：[0，1]

点评 本题主要考查函数定义域的求解，根据复合函数定义域之间的关系建立不等式关系是解决本题的关键．

练习册系列答案
相关题目
10．已知函数f（x）=$\frac{1}{{2}^{x}-1}$+$\frac{1}{2}$，
（1）求f（x）的定义域；
（2）判断函数f（x）的奇偶性．
11．已知直线l过点P（3，-2）且与椭圆$C：\frac{x^2}{20}+\frac{y^2}{16}=1$相交于A，B两点，则使得点P为弦AB中点的直线斜率为（　　）
A．$-\frac{3}{5}$B．$-\frac{6}{5}$C．$\frac{6}{5}$D．$\frac{3}{5}$
8．不等式logax-ln2x＜4（a＞0，且a≠1）对任意x∈（1，100）恒成立，则实数a的取值范围为（0，1）∪（${e}^{\frac{1}{4}}$，+∞）．
15．函数$y={log_a}{x^2}$的零点为（　　）
A．±1B．（±1，0）C．1D．（1，0）
5．已知α是第四象限角，sin（$\frac{5π}{2}$+α）=$\frac{1}{5}$，那么tan α等于（　　）
A．-$\frac{2\sqrt{6}}{5}$B．-2$\sqrt{6}$C．2$\sqrt{6}$D．$\frac{2\sqrt{6}}{5}$
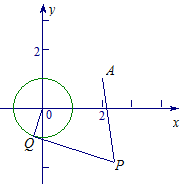12．已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P（a，b）向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|．
（Ⅰ）求实数a、b间满足的等量关系；
（Ⅱ） 求线段PQ长的最小值；
（Ⅲ） 若以P为圆心所作的圆P与圆O有公共点，试求半径取最小值时圆P的方程．
9．已知椭圆：C：$\frac{{x}^{2}}{9}$+y2=1，点M（0，$\frac{1}{2}$）．
（1）设P是椭圆C上任意的一点，Q是点P关于坐标原点的对称点，记λ=$\overrightarrow{MP}$•$\overrightarrow{MQ}$，求λ的取值范围；
（2）已知点D（-1，-$\frac{1}{2}$），E（1，-$\frac{1}{2}$），P是椭圆C上在第一象限内的点，记l为经过原点与点P的直线，s为△DEM截直线l所得的线段长，试将s表示成直线l的斜率k的函数．
10．设集合 M={x||x|≤2，x∈R}，N={x|x2≤4，x∈N}，则（　　）
A．M=NB．M?NC．M?ND．M∩N=∅

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网