题目内容
2.求下列各式的值:(1)cos$\frac{25π}{3}$+tan($\frac{15π}{4}$);
(2)sin810°+tan765°-cos360°.
分析 (1)原式中的角度变形后,利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果;
(2)原式中的角度变形后,利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果.
解答 解:(1)原式=cos(8π+$\frac{π}{3}$)+tan(4π-$\frac{π}{4}$)=cos$\frac{π}{3}$-tan$\frac{π}{4}$=$\frac{1}{2}$-1=-$\frac{1}{2}$;
(2)原式=sin(720°+90°)+tan(720°+45°)-cos360°=sin90°+tan45°-cos360°=1+1-1=1.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
7.若不等式组$\left\{\begin{array}{l}{x+ay+1≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$,表示的平面区域的面积等于4,则a=( )
| A. | 1 | B. | -1 | C. | 0 | D. | 2 |
13.“因为如果一条直线平行于一个平面,则该直线平行于平面内的所有直线(大前提),而直线b∥平面α,直线a?平面α(小前提),则直线b∥直线a(结论).”上面推理的错误是( )
| A. | 大前提错导致结论错 | B. | 小前提错导致结论错 | ||
| C. | 推理形式错导致结论错 | D. | 大前提和小前提错导致结论错 |
7.用反证法证明命题“设a,b为实数,则方程x3+ax2+b=0至少有一个实根”时,要做的假设是( )
| A. | 方程x3+ax2+b=0至多有一个实根 | B. | 方程x3+ax2+b=0没有实根 | ||
| C. | 方程x3+ax2+b=0至多有两个实根 | D. | 方程x3+ax2+b=0恰好有两个实根 |
11.将函数f(x)=2sin(2x-$\frac{π}{4}$)的图象向左平移$\frac{π}{4}$个单位,得到函数g(x)的图象,则g(0)=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 0 | D. | -$\sqrt{2}$ |
 已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切.
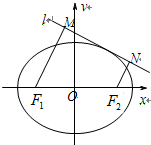
已知椭圆C的中心在坐标原点,左、右焦点分别为F1,F2,P为椭圆C上的动点,△PF1F2的面积最大值为$\sqrt{3}$,以原点为圆心,椭圆短半轴长为半径的圆与直线y=$\sqrt{3}$(x+2)相切. 如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,D,E是椭圆的两个顶点,|F1F2|=2$\sqrt{3}$,|DE|=$\sqrt{5}$,若点M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知以PQ为直径的圆经过坐标原点O.
如图,F1,F2为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,D,E是椭圆的两个顶点,|F1F2|=2$\sqrt{3}$,|DE|=$\sqrt{5}$,若点M(x0,y0)在椭圆C上,则点N($\frac{{x}_{0}}{a}$,$\frac{{y}_{0}}{b}$)称为点M的一个“椭点”.直线l与椭圆交于A,B两点,A,B两点的“椭点”分别为P,Q,已知以PQ为直径的圆经过坐标原点O.