题目内容
10.对于a>0,b>0,下列不等式中不正确的是( )| A. | $\frac{\sqrt{ab}}{2}$<$\frac{1}{a}$+$\frac{1}{b}$ | B. | ab≤$\frac{{a}^{2}+{b}^{2}}{2}$ | C. | ab≤($\frac{a+b}{2}$)2 | D. | ($\frac{a+b}{2}$)2≤$\frac{{a}^{2}+{b}^{2}}{2}$ |
分析 选项A取反例可得,选项BC由基本不等式可得,选项D作差法可得.
解答 解:选项A,取a=b=2,可得$\frac{\sqrt{ab}}{2}$=1,$\frac{1}{a}+\frac{1}{b}$=1,不满足$\frac{\sqrt{ab}}{2}$<$\frac{1}{a}+\frac{1}{b}$,故错误;
选项B,由基本不等式可得2ab≤a2+b2,变形可得ab≤$\frac{{a}^{2}+{b}^{2}}{2}$,当且仅当a=b时取等号,故正确;
选项C,由基本不等式可得$\sqrt{ab}$≤$\frac{a+b}{2}$,平方可得ab≤($\frac{a+b}{2}$)2,当且仅当a=b时取等号,故正确;
选项D,作差可得($\frac{a+b}{2}$)2-$\frac{{a}^{2}+{b}^{2}}{2}$=$\frac{{a}^{2}+{b}^{2}+2ab}{4}$-$\frac{{a}^{2}+{b}^{2}}{2}$=$\frac{-{a}^{2}-{b}^{2}+2ab}{4}$=-$\frac{(a-b)^{2}}{4}$≤0,当且仅当a=b时取等号,故正确.
故选:A
点评 本题考查不等式比较大小,涉及基本不等式和作差法,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.空间直角坐标系中点P(1,2,3)关于y轴的对称点的坐标为( )
| A. | (3,2,1) | B. | (1,-2,3) | C. | (-1,2,-3) | D. | (1,2,3) |
15.已知集合A={x2-5x-6<0},B={x|2x<1},则图中阴影部分表示的集合是( )
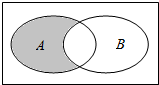

| A. | {x|2<x<3} | B. | {x|-1<x≤0} | C. | {x|0≤x<6} | D. | {x|x<-1} |
2.定义在R的奇函数f(x),当x∈(-∞,0)时,f(x)+xf′(x)<0恒成立,若a=(log3π)•f(log3π),b=(logπ3)•f(logπ3),c=(-lnπ)•f(-lnπ),则( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |