题目内容
1.已知AC、BD分别为圆O:x2+y2=4的两条垂直于坐标轴的弦,且AC、BD相交于点M(1,$\sqrt{2}$),则四边形ABCD的面积为( )| A. | 2$\sqrt{6}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | $\frac{3\sqrt{2}}{2}$ |
分析 求出|AC|,|BD|,代入面积公式S=$\frac{1}{2}$•|AC||BD|,即可求出四边形ABCD的面积.
解答 解:由题意圆心O到AC、BD的距离分别为$\sqrt{2}$、1,
∴|AC|=2$\sqrt{4-2}$=2$\sqrt{2}$,|BD|=$\sqrt{4-1}$=2$\sqrt{3}$,
∴四边形ABCD的面积为:S=$\frac{1}{2}$•|AC|(|BM|+|MD|)=$\frac{1}{2}$•|AC||BD|=$\frac{1}{2}×2\sqrt{2}×2\sqrt{3}$=2$\sqrt{6}$,
故选:A.
点评 此题考查四边形ABCD的面积.解答关键是四边形面积可用S=$\frac{1}{2}$•|AC||BD|来计算.

练习册系列答案
相关题目
6.等比数列{an}中,a1+a2=4,a2+a3=12,则a3与a4的等差中项为( )
| A. | 6 | B. | 12 | C. | 9 | D. | 18 |
13.下列判断错误的是( )
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“x∈R,x3-x2-1≤0”的否定是“?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$-1>0” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 函数y=1是幂函数 |
 如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD
如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD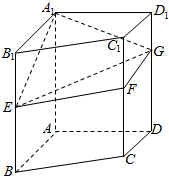 如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.
如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.