题目内容
已知数列{2n-1•an}的前n项和Sn=9-6n.
(1)求数列{an}的通项公式;
(2)设bn=n(3-log2
),设数列{
}的前n项和为Tn,是否存在最大的整数m,使得对任意n∈N*均有Tn>
成立.若存在,求出m的值;若不存在,说明理由.
(1)求数列{an}的通项公式;
(2)设bn=n(3-log2
| |an| |
| 3 |
| 1 |
| bn |
| m |
| 27 |
(1)由题意,2n-1•an=Sn-Sn-1=(9-6n)-(15-6n)=-6
∴an=-6•21-n;
(2)bn=n(3-log2
)=n(n+1)
∴
=
=
-
∴Tn=1-
+
-
+…+
-
=1-
∵对任意n∈N*均有Tn>
成立
∴
>
∴m<
∴m的最大整数为13.
∴an=-6•21-n;
(2)bn=n(3-log2
| |an| |
| 3 |
∴
| 1 |
| bn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
∵对任意n∈N*均有Tn>
| m |
| 27 |
∴
| 1 |
| 2 |
| m |
| 27 |
∴m<
| 27 |
| 2 |
∴m的最大整数为13.

练习册系列答案
相关题目
 ,求数列
,求数列 的前n项和.
的前n项和.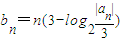 ,求数列
,求数列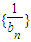 的前n项和.
的前n项和.