题目内容
已知数列{2n-1•an}的前n项和Sn=9-6n.
(1)求数列{an}的通项公式.
(2)设bn=n(3-log2
),求数列{
}的前n项和.
(3)数列{cn}的首项c1=1,且cn-2cn-1=|an|(n≥2),求数列{cn}的通项公式.
(1)求数列{an}的通项公式.
(2)设bn=n(3-log2
| |an| |
| 3 |
| 1 |
| bn |
(3)数列{cn}的首项c1=1,且cn-2cn-1=|an|(n≥2),求数列{cn}的通项公式.
分析:(1)利用an=
即可得出;
(2)利用“裂项求和”即可得出;
(3)变形转化为等比数列,利用其通项公式即可得出.
|
(2)利用“裂项求和”即可得出;
(3)变形转化为等比数列,利用其通项公式即可得出.
解答:解:(1)n=1时,20•a1=S1=9-6,∴a1=3.
n≥2时,2n-1•an=Sn-Sn-1=9-6n-[9-6(n-1)]=-6,∴an=
.
∴通项公式an=
.
(2)当n=1时,b1=3-lo
=3,∴
=
.
n≥2时,bn=n(3-lo
)=n(n+1),∴
=
=
-
.
∴
+
+…=
=
+
+
+…+
=
+(
-
)+(
-
)+…+(
-
)
=
-
=
(n=1时也成立).
(3)∵c1=1,且cn-2cn-1=|an|(n≥2),∴n=2时,c2-2c1=|a2|=3,∴c2=5,
n>2时,cn=2cn-1+
两边同时乘以2n,得2ncn=4×2n-1cn-1+12,即2n(cn+4)=4×(2n-1cn-1+4).
∴数列{2ccn+4}是以6为首项,4为公比的等比数列,2ncn+4=6×4n-1,∴cn=3×2n-1-22-n(n≥2).
又C1=1,满足上式.
∴通项公式为cn=3×2n-1-22-n(n≥2).
n≥2时,2n-1•an=Sn-Sn-1=9-6n-[9-6(n-1)]=-6,∴an=
| -3 |
| 2n-2 |
∴通项公式an=
|
(2)当n=1时,b1=3-lo
| g |
2 |
| 1 |
| b1 |
| 1 |
| 3 |
n≥2时,bn=n(3-lo
| g |
2 |
| 1 |
| bn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 3 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 5 |
| 6 |
| 1 |
| n+1 |
| 5n-1 |
| 6(n+1) |
(3)∵c1=1,且cn-2cn-1=|an|(n≥2),∴n=2时,c2-2c1=|a2|=3,∴c2=5,
n>2时,cn=2cn-1+
| 3 |
| 2n-2 |
∴数列{2ccn+4}是以6为首项,4为公比的等比数列,2ncn+4=6×4n-1,∴cn=3×2n-1-22-n(n≥2).
又C1=1,满足上式.
∴通项公式为cn=3×2n-1-22-n(n≥2).
点评:数列掌握“利用an=
求an”、裂项求和”、变形转化为等比数列等是解题的关键.
|

练习册系列答案
相关题目
 ,求数列
,求数列 的前n项和.
的前n项和.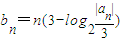 ,求数列
,求数列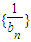 的前n项和.
的前n项和.