题目内容
已知数列{2n-1•an}的前n项和Sn=9-6n
(1)求数列{an}的通项公式.
(2)设bn=n(3-log2
),求数列{
}的前n项和.
(1)求数列{an}的通项公式.
(2)设bn=n(3-log2
| |an| |
| 3 |
| 1 |
| bn |
分析:(1)先根据数列{2n-1•an}的前n项和Sn=9-6n求出数列{2n-1•an}的通项公式,再计算数列{an}的通项公式.
(2)根据bn=n(3-log2
),以及(1)中求出的数列{an}的通项公式,求出数列{bn}的通项公式,再求出数列{
}的通项公式,最后利用裂项相消法求前n项和.
(2)根据bn=n(3-log2
| |an| |
| 3 |
| 1 |
| bn |
解答:解:(1)n=1时,20•a1=S1=3∴a1=3
n≥2时,2n-1•an=Sn-Sn-1=-6∴an=
∴通项公式an=
(2)当n=1时,b1=3-log2
=3∴
=
n≥2时,bn=n(3-log2
)=n(n+1)
∴
=
∴
+
+
+…+
=
+
+
+…+
=
-
=
n≥2时,2n-1•an=Sn-Sn-1=-6∴an=
| -3 |
| 2n-2 |
∴通项公式an=
|
(2)当n=1时,b1=3-log2
| 3 |
| 3 |
| 1 |
| b1 |
| 1 |
| 3 |
n≥2时,bn=n(3-log2
| 3 |
| 3•2n-2 |
∴
| 1 |
| bn |
| 1 |
| n(n+1) |
∴
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
| 1 |
| 3 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 5 |
| 6 |
| 1 |
| n+1 |
| 5n-1 |
| 6(n+1) |
点评:本题考查了构造法求数列的通项公式,以及裂项相消法求数列的和.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 ,求数列
,求数列 的前n项和.
的前n项和.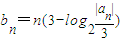 ,求数列
,求数列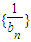 的前n项和.
的前n项和.