题目内容
6.若已知数列{an}满足$\frac{1+2+3+…+n}{{a}_{1}+{a}_{2}+{a}_{3}+…{a}_{n}}$=$\frac{1}{2}$,则an=( )| A. | -2n | B. | 2n | C. | -4n | D. | 4n |
分析 把已知数列递推式变形,可得${S}_{n}={n}^{2}+n$,求出首项,再由an=Sn-Sn-1(n≥2)求得数列的通项公式.
解答 解:由$\frac{1+2+3+…+n}{{a}_{1}+{a}_{2}+{a}_{3}+…{a}_{n}}$=$\frac{1}{2}$,得$\frac{\frac{n(n+1)}{2}}{{S}_{n}}=\frac{1}{2}$,
∴${S}_{n}={n}^{2}+n$,
当n=1时,a1=S1=2;
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}={n}^{2}+n-(n-1)^{2}-(n-1)=2n$,
验证n=1时上式成立,
∴an=2n.
故选:B.
点评 本题考查数列递推式,训练了由数列的前n项和求数列的通项公式,是中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.已知实数x,y满足$\left\{\begin{array}{l}{x+y≥2}\\{x+2y≥3}\\{x≥0}\\{y≥0}\end{array}\right.$,则x+3y的最小值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.已知$cos2α=\frac{3}{7}$且cosα<0,tanα<0,则sinα等于( )
| A. | $-\frac{{\sqrt{14}}}{7}$ | B. | $\frac{{\sqrt{14}}}{7}$ | C. | $-\frac{{2\sqrt{7}}}{7}$ | D. | $\frac{{2\sqrt{7}}}{7}$ |
1.集合P={x|x≥3或x≤-3},Q={y|y>-1},则P∩Q=( )
| A. | [3,+∞) | B. | (-∞,-3]∪(-1,+∞) | C. | (-1,+∞) | D. | (-∞,-1)∪[3,+∞) |
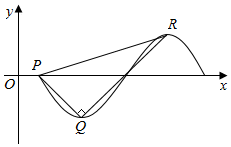 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )