题目内容

如图所示,A,B,C,D四点在平面M和N之外,它们在M内的射影A1,B1,C1,D1成一直线,在N内的射影A2,B2,C2,D2组成一个平行四边形,求证:ABCD是平行四边形.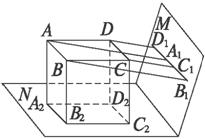

证明:∵A,B,C,D四点在平面M内的射影是一条直线,

∴ABCD为平面四边形.

又AA2⊥平面N,DD2⊥平面N,

∴AA2∥DD2.

∵A2B2∥C2D2,

∴平面AA2B2B∥平面CC2D2D.

又ABCD为平面四边形,

∴AB∥CD.

同理可证AD∥BC.

∴ABCD为平行四边形.

练习册系列答案
相关题目
向量
a
，
b
，
c
在正方形网格中的位置如图所示，若
c
=λ
a
+μ
b
(λ，μ∈R)，则λ+μ=
-
5
2
-
5
2
．
如图所示，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率e=
2
2
，左焦点为F1（-1，0），右焦点为F2（1，0），短轴两个端点为A、B．与x轴不垂直的直线l与椭圆C交于不同的两点M、N，记直线AM、AN的斜率分别为k1、k2，且k1k2=
3
2
．
（1）求椭圆C的方程；
（2）求证直线l与y轴相交于定点，并求出定点坐标．
（3）当弦MN的中点P落在△MF1F2内（包括边界）时，求直线l的斜率的取值．
（2010•茂名二模）如图所示，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
2
5
5
，且A（0，1）是椭圆C的顶点．
（1）求椭圆C的方程；
（2）过点A作斜率为1的直线l，在直线l上求一点M，使得以椭圆C的焦点为焦点，且过点M的双曲线E的实轴最长，并求此双曲线E的方程．

已知两直线的方程分别为l1：x+ay+b=0，l2：x+cy+d=0，它们在坐标系中的位置如图所示


  1. A.
    b＞0，d＜0，a＜c
  2. B.
    b＞0，d＜0，a＞c
  3. C.
    b＜0，d＞0，a＜c
  4. D.
    b＜0，d＞0，a＞c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网