题目内容
18．已知等差数列{an}的前n项和为Sn，且2（a1+a3+a5）+3（a8+a10）=36，则S11=（ ）| A． | 66 | B． | 55 | C． | 44 | D． | 33 |
分析 利用等差数列等差数列通项公式求出a1+5d=3．即a6=3，由此能求出S11的值．
解答 解：∵Sn是等差数列{an}的前n项和，2（a1+a3+a5）+3（a8+a10）=36，
∴2（a1+a1+2d+a1+4d）+3（a1+7d+a1+9d）=36，
解得a1+5d=3．∴a6=3，
∴S11=$\frac{11}{2}（{a}_{1}+{a}_{11}）$=$\frac{11}{2}×2{a}_{6}$=11a6=33．
故选：D．
点评 本题考查数列的第31项的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
8．某单位生产A、B两种产品，需要资金和场地，生产每吨A种产品和生产每吨B种产品所需资金和场地的数据如表所示：
现有资金12万元，场地400平方米，生产每吨A种产品可获利润3万元；生产每吨B种产品可获利润2万元，分别用x，y表示计划生产A、B两种产品的吨数．
（1）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（2）问A、B两种产品应各生产多少吨，才能产生最大的利润？并求出此最大利润．
| 资源 产品 | 资金（万元） | 场地（平方米） |
| A | 2 | 100 |
| B | 3 | 50 |
（1）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（2）问A、B两种产品应各生产多少吨，才能产生最大的利润？并求出此最大利润．
6．执行如图所示的程序框图，则输出S=（ ）
| A． | 4 | B． | log215 | C． | log217 | D． | 3 |
3．
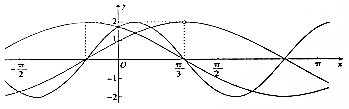已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）
已知ω＞0，a＞0，f（x）=asinωx+$\sqrt{3}$acosωx，g（x）=2cos（ax+$\frac{π}{6}$），h（x）=$\frac{f（x）}{g（x）}$这3个函数在同一直角坐标系中的部分图象如图所示，则函数g（x）+h（x）的图象的一条对称轴方程可以为（ ）| A． | x=$\frac{π}{6}$ | B． | x=$\frac{13π}{6}$ | C． | x=-$\frac{23π}{12}$ | D． | x=-$\frac{29π}{12}$ |
10．已知集合A={-2，-1，0，1，2}，B={x|lgx≤0}，则A∩B=（ ）
| A． | {1} | B． | {0，1} | C． | {0，1，2} | D． | {1，2} |
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，以F1F2为直径的圆与双曲线渐近线的一个交点为（3，4），则此双曲线的方程为（ ）
| A． | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B． | $\frac{x^2}{3}-\frac{y^2}{4}=1$ | C． | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | D． | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |