题目内容
11.已知⊙C:x2+(y-1)2=5,直线l:mx-y+1-m=0.(1)求证:对任意实数m,直线与⊙C总有两个不同的公共点;
(2)求直线被⊙C截得的线段最短时直线的方程.
分析 (1)确定直线l恒过定点A(1,1),定点A(1,1)在圆内,即可证明直线l与圆C相交;
(2)直线被⊙C截得的线段最短时,CA⊥l,即可得出结论.
解答 (1)证明:∵直线l的方程为mx-y+1-m=0,
∴m(x-1)-y+1=0,
令x-1=0,-y+1=0,∴x=1,y=1,
∴直线l恒过定点A(1,1),
∴12+(1-1)2=1<5,
∴定点A(1,1)在圆内,
∴直线l与圆C相交;
(2)解:直线被⊙C截得的线段最短时,CA⊥l,
∵kCA=0,
∴直线l的方程为x=1.
点评 本题主要考查直线和圆的位置关系的判定,直线过定点问题,求点的轨迹方程,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.某三棱锥的三视图如图所示,其体积V=( )
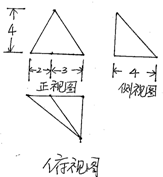

| A. | $\frac{80}{\begin{array}{l}3\end{array}}$ | B. | $\frac{40}{\begin{array}{l}3\end{array}}$ | C. | 80 | D. | 40 |
1.不等式2x2-axy+3y2≥0对于任意x∈[1,2]及y∈[1,3]恒成立,则实数a的取值范围是( )
| A. | a≤2$\sqrt{2}$ | B. | a≤2$\sqrt{6}$ | C. | a≤5 | D. | a≤$\frac{9}{2}$ |