题目内容
19.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个不共线向量,若向量$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,与$\overrightarrow{a}$=$2\overrightarrow{{e}_{1}}$-λ$\overrightarrow{{e}_{2}}$共线,则实数λ=-2.分析 根据$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个不共线向量,作为基底表示出$\overrightarrow{b}$与$\overrightarrow{a}$,再利用共线定理列出方程求出λ的值.
解答 解:$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是两个不共线向量,作为基底时,
向量$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$=(1,1),
$\overrightarrow{a}$=$2\overrightarrow{{e}_{1}}$-λ$\overrightarrow{{e}_{2}}$=(2,-λ),
且$\overrightarrow{b}$与$\overrightarrow{a}$共线,
∴1×(-λ)-2×1=0,
解得λ=-2.
故答案为:-2.
点评 本题考查了平面向量的坐标表示与共线定理的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.i是虚数单位,设复数z满足|z|=1,则|$\frac{{z}^{2}-2z+2}{z-1+i}$|的最大值为( )
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | 2+$\sqrt{2}$ |
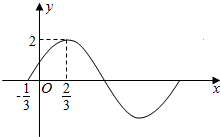 己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)部分图象如图所示.