题目内容
8.已知命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立,命题q:f(x)=(4-3a)x是增函数,若p或q为真,p且q为假.求实数a的取值范围.分析 当命题p为真时,△<0.当命题q为真时,4-3a>1.由p或q为真,p且q为假,p,q为一真一假,即可得出.
解答 解:当命题p为真时,△=4a2-16<0,(1分) 所以-2<a<2.(2分)
当命题q为真时,4-3a>1,(3分)所以a<1. (4分)
因为p或q为真,p且q为假,p,q为一真一假.(5分)
当p真q假时,$\left\{\begin{array}{l}{-2<a<2}\\{a≥1}\end{array}\right.$,(6分)
所以1≤a<2. (7分)
当p假q真时,$\left\{\begin{array}{l}{a≤-2或a≥2}\\{a<1}\end{array}\right.$,(8分)
所以a≤-2(9分)
综上所述,实数a的取值范围是(-∞,-2]∪[1,2). ((10分))
点评 本题考查了不等式的解法、不等式的解集与判别式的关系、复合命题真假的判定方法、函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.在高三一次数学测验后,某班对选做题的选题情况进行了统计,如表.
(Ⅰ)求全班选做题的均分;
(Ⅱ)据此判断是否有90%的把握认为选做《坐标系与参数方程》或《不等式选讲》与性别有关?
(Ⅲ)已知学习委员甲(女)和数学科代表乙(男)都选做《不等式选讲》.若在《不等式选讲》中按性别分层抽样抽取3人,记甲乙两人被选中的人数为,求的数学期望.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,n=a+b+c+d.
下面临界值表仅供参考:
| 坐标系与参数方程 | 不等式选讲 | |||
| 人数及均分 | 人数 | 均分 | 人数 | 均分 |
| 男同学 | 14 | 8 | 6 | 7 |
| 女同学 | 8 | 6.5 | 12 | 5.5 |
(Ⅱ)据此判断是否有90%的把握认为选做《坐标系与参数方程》或《不等式选讲》与性别有关?
(Ⅲ)已知学习委员甲(女)和数学科代表乙(男)都选做《不等式选讲》.若在《不等式选讲》中按性别分层抽样抽取3人,记甲乙两人被选中的人数为,求的数学期望.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,n=a+b+c+d.
下面临界值表仅供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.“x<2”是“2x<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.已知平面区域$Ω:\left\{{\begin{array}{l}{3x+4y-18≤0}\\{x≥2}\\{y≥0}\end{array}}\right.$,夹在两条斜率为$-\frac{3}{4}$的平行直线之间,且这两条平行直线间的最短距离为m.若点P(x,y)∈Ω,则z=mx-y的最小值为( )
| A. | $\frac{9}{5}$ | B. | 3 | C. | $\frac{24}{5}$ | D. | 6 |
13.双曲线实半轴长为2,焦点为(-3,0)、(3,0),则该双曲线为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
18.设全集U={0,1,2,3,4},集合A={0,1,3},集合B={2,3},则∁U(A∪B)=( )
| A. | {4} | B. | {0,1,2,3} | C. | {3} | D. | {0,1,2,4} |
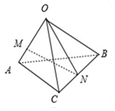 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)