题目内容
已知函数f(x)=2
sin
xcos
x+2
cos2
x-
,x∈R.
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若函数f(x)图象上的两点P,Q的横坐标依次为2,4,O为坐标原点,求△OPQ的外接圆的面积.
| 2 |
| π |
| 8 |
| π |
| 8 |
| 2 |
| π |
| 8 |
| 2 |
(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若函数f(x)图象上的两点P,Q的横坐标依次为2,4,O为坐标原点,求△OPQ的外接圆的面积.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)借助于二倍角公式和辅助角公式化简函数解析式为:f(x)=2sin(
x+
),从而根据周期公式求解周期,根据三角函数的单调性求解单调递增区间;
(Ⅱ)确定f(2)、f(4)的值,得到P(2,
),Q(4,-
),然后利用余弦定理求解
∠POQ的大小,最后,根据正弦定理的推论求解.
| π |
| 4 |
| π |
| 4 |
(Ⅱ)确定f(2)、f(4)的值,得到P(2,
| 2 |
| 2 |
∠POQ的大小,最后,根据正弦定理的推论求解.
解答:
解:(Ⅰ)f(x)=2
sin
xcos
x+
(2cos2
x-1)=
sin
x+
cos
x=2sin(
x+
),
∴f(x)=2sin(
x+
)
∴T=
=8.
∴函数f(x)的最小正周期为8.
由2kπ-
≤
x+
≤2kπ+
(k∈Z),
得8k-3≤x≤8k+1(k∈Z),
∴函数f(x)的单调递增区间是[8k-3,8k+1](k∈Z).
(Ⅱ)∵f(2)=2sin(
+
)=2cos
=
,
f(4)=2sin(π+
)=-2sin
=-
,
∴P(2,
),Q(4,-
),
∴|OP|=
,|PQ|=2
,|OQ|=3
从而cos∠POQ=
=
=
,
∴sin∠POQ=
=
,
设△OPQ的外接圆的半径为R,
由
=2R⇒R=
=
=
,
∴△OPQ的外接圆的面积S=πR2=
π.
| 2 |
| π |
| 8 |
| π |
| 8 |
| 2 |
| π |
| 8 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∴f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
∴T=
| 2π | ||
|
∴函数f(x)的最小正周期为8.
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
得8k-3≤x≤8k+1(k∈Z),
∴函数f(x)的单调递增区间是[8k-3,8k+1](k∈Z).
(Ⅱ)∵f(2)=2sin(
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
f(4)=2sin(π+
| π |
| 4 |
| π |
| 4 |
| 2 |
∴P(2,
| 2 |
| 2 |
∴|OP|=
| 6 |
| 3 |
| 2 |
从而cos∠POQ=
| ||||
|
|
2×4+
| ||||
|
| ||
| 3 |
∴sin∠POQ=
| 1-cos2∠POQ |
| ||
| 3 |
设△OPQ的外接圆的半径为R,
由
| |PQ| |
| sin∠POQ |
| |PQ| |
| 2sin∠POQ |
2
| ||||
2×
|
3
| ||
| 2 |
∴△OPQ的外接圆的面积S=πR2=
| 9 |
| 2 |
点评:本题重点考查了三角函数的图象与性质、二倍角公式、辅助角公式、解三角形等知识,属于综合题目.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
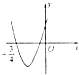 如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
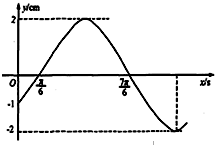 如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-
如图是某简谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-