题目内容
11.根据已知条件求方程:(1)求与椭圆$\frac{{x}^{2}}{40}$+$\frac{{y}^{2}}{15}$=1有相同焦点,且离心率$e=\frac{5}{4}$的双曲线的标准方程.
(2)已知椭圆的中心在原点,且过点P(3,2),焦点在x轴上,长轴长是短轴长的3倍,求该椭圆的方程.
分析 (1)设要求的双曲线的标准方程为$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{25-m}$=1(m,25-m>0),可得e=$\frac{5}{4}$=$\frac{c}{a}$=$\sqrt{1+\frac{25-m}{m}}$,解得m即可得出.
(2)设要求的椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),可得$\frac{9}{{a}^{2}}+\frac{4}{{b}^{2}}$=1,2a=3×2b,解出即可得出.
解答 解:(1)设与椭圆$\frac{{x}^{2}}{40}$+$\frac{{y}^{2}}{15}$=1有相同焦点,且离心率$e=\frac{5}{4}$的双曲线的标准方程为$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{25-m}$=1(m,25-m>0),则e=$\frac{5}{4}$=$\frac{c}{a}$=$\sqrt{1+\frac{25-m}{m}}$,解得m=16.
∴要求的双曲线标准方程为:$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=1.
(2)设要求的椭圆标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则$\frac{9}{{a}^{2}}+\frac{4}{{b}^{2}}$=1,2a=3×2b,解得b2=5,a2=45.
∴椭圆的标准方程为:$\frac{{x}^{2}}{45}+\frac{{y}^{2}}{5}$=1.
点评 本题考查了椭圆与双曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
①AC⊥BD;②△ADC是正三角形;③AB与CD成60°角;④AB与平面BCD成60°角.
则其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $({\frac{{\sqrt{3}}}{2}})$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
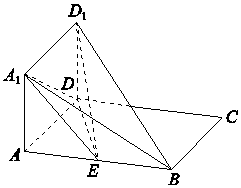 如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.
如图所示,四边形ABCD和四边形ADD1A1均为矩形且所在的平面互相垂直,E为线段AB的中点.