题目内容
在△ABC中，若sinAcosB＜0，则此三角形必是
- A.锐角三角形
- B.任意三角形
- C.直角三角形
- D.钝角三角形
D
分析：由sinAcosB＜0，结合0＜A＜π可得sinA＞0，从而有 cosB＜0，则可得B为钝角，即可得答案．
解答：∵sinAcosB＜0
又∵0＜A＜π∴sinA＞0
∵sinAcosB＜0
∴cosB＜0
∴π＞B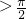
∴B为钝角，
则此三角形必是钝角三角形．
故选D．
点评：本题主要是利用三角形的内角范围及正弦函数的性质判定三角形的形状，属于简单题．
分析：由sinAcosB＜0，结合0＜A＜π可得sinA＞0，从而有 cosB＜0，则可得B为钝角，即可得答案．
解答：∵sinAcosB＜0
又∵0＜A＜π∴sinA＞0
∵sinAcosB＜0
∴cosB＜0
∴π＞B
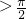
∴B为钝角，
则此三角形必是钝角三角形．
故选D．
点评：本题主要是利用三角形的内角范围及正弦函数的性质判定三角形的形状，属于简单题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
在△ABC中，若sinA=
，cosB=
，则cosC的值是（ ）
| 3 |
| 5 |
| 5 |
| 13 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
在△ABC中，若sinA：sinB：sinC=5：7：8，则此三角形的最大角与最小角之和为（ ）
| A、90° | B、120° | C、135° | D、150° |