题目内容
下面有5个命题:①分针每小时旋转2π弧度;
②若
| OA |
| OB |
| OC |
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④函数f(x)=
| sinx |
| 1+cosx |
⑤在△ABC中,若sinA=sinB,则A=B.
其中,真命题的编号是
分析:根据正负角的定义,可以判断①的真假;根据向量法判断平面上三点共线的条件,可以判断②的真假;根据正弦函数的图象和性质,可以判断③的真假;根据函数奇偶性的定义,可以判断④的真假,根据正弦定理推论(边角互化),易判断⑤的真假;进而得到答案.
解答:解:分针每小时旋转-2π弧度,故①错误;
若
=x
+y
,且x+y=1,则A,B,C三点共线,故②正确;
在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点,故③错误;
∵函数f(-x)=
=-
=-f(x),故f(x)=
是奇函数,故④正确;
在△ABC中,sinA=sinB?A=B,故⑤正确.
故答案为:②④⑤
若
| OA |
| OB |
| OC |
在同一坐标系中,函数y=sinx的图象和函数y=x的图象有一个公共点,故③错误;
∵函数f(-x)=
| sin(-x) |
| 1+cos(-x) |
| sinx |
| 1+cosx |
| sinx |
| 1+cosx |
在△ABC中,sinA=sinB?A=B,故⑤正确.
故答案为:②④⑤
点评:本题考查的知识点是命题的真假判断及其应用,正负角的定义,三点共线的判定,正弦函数的图象和性质,函数奇偶性的定义,正弦定理,熟练掌握上述基础知识,并判断出题目中4个命题的真假,是解答本题的关键.

练习册系列答案
相关题目
 弧度;
弧度; ,且
,且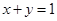 ,则
,则 三点共线;
三点共线; 的图象和函数
的图象和函数 的图象有三个公共点;
的图象有三个公共点; 是奇函数;
是奇函数; 中,若
中,若 ,则
,则 。
。 是奇函数;
是奇函数; ,且x+y=1,则A,B,C三点共线;
,且x+y=1,则A,B,C三点共线;