题目内容
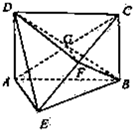 (2013•湛江一模)如图,矩形ABCD中,对角线AC、BD的交点为G,AD⊥平面ABE,AE⊥EB,AE=EB=BC=2,F为CE上的点,且BF⊥CE.
(2013•湛江一模)如图,矩形ABCD中,对角线AC、BD的交点为G,AD⊥平面ABE,AE⊥EB,AE=EB=BC=2,F为CE上的点,且BF⊥CE.(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-GBF的体积.
分析:(1)利用线面垂直的性质及判定可得BC⊥平面ABE,可得BC⊥AE.再利用线面垂直的判定定理可得AE⊥平面BCE;
(2)利用矩形的性质可得AG=GC,利用等腰三角形的性质可得EF=FC,再利用线面平行的判定定理可得AE∥平面BFD.
(3)由三角形的中位线定理可得:FG∥AE,FG=
AE=1.利用线面垂直的性质可得FG⊥平面BCE.再利用“等体积变形”即可得出VC-GBF=VG-BCF计算出即可.
(2)利用矩形的性质可得AG=GC,利用等腰三角形的性质可得EF=FC,再利用线面平行的判定定理可得AE∥平面BFD.
(3)由三角形的中位线定理可得:FG∥AE,FG=
| 1 |
| 2 |
解答:证明:(1)∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE,∴BC⊥AE.
又∵AE⊥EB,EB∩BC=B,∴AE⊥平面BCE;
(2)∵G是矩形ABCD的对角线AC、BD的交点,∴AG=GC.
在△EBC中,∵EB=BC,BF⊥CE,∴EF=FC.
∴FG∥AE.
又FG?平面BFD,AE?平面BFD,
∴AE∥平面BFD.
(3)解:由三角形的中位线定理可得:FG∥AE,FG=
AE=1.
∵AE⊥平面BCE,∴FG⊥平面BCE.
Rt△BCE中,EB=BC=2,F是EC的中点,
∴S△BCF=
S△BCE=
×
×22=1,
∴VC-GBF=VG-BCF=
×GF×S△BCF=
×1×1=
.
又∵AE⊥EB,EB∩BC=B,∴AE⊥平面BCE;
(2)∵G是矩形ABCD的对角线AC、BD的交点,∴AG=GC.
在△EBC中,∵EB=BC,BF⊥CE,∴EF=FC.
∴FG∥AE.
又FG?平面BFD,AE?平面BFD,
∴AE∥平面BFD.
(3)解:由三角形的中位线定理可得:FG∥AE,FG=
| 1 |
| 2 |
∵AE⊥平面BCE,∴FG⊥平面BCE.
Rt△BCE中,EB=BC=2,F是EC的中点,
∴S△BCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴VC-GBF=VG-BCF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题中考查了线面平行于垂直的判定定理和性质定理、三角形的中位线定理、三棱锥的体积计算公式及“等体积变形”等基础知识和基本技能,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 (2013•湛江一模)如图圆上的劣弧
(2013•湛江一模)如图圆上的劣弧