题目内容
已知平面上不同的四点A、B、C、D，若
•
+
•
+
•
=0，则三角形ABC一定是（ ）
| DB |
| DC |
| CD |
| DC |
| DA |
| BC |
分析：由向量的数量积的运算可化简原式，可得
•
=0，进而可得垂直，可得直角，可得答案．
| CA |
| BC |
解答：解：
•
+
•
+
•
=（
+
）•
+
•
=
•
+
•
=
•
+
•
=（
+
）•
=
•
=0，
故可得
⊥
，即∠ACB为直角，
故选D
| DB |
| DC |
| CD |
| DC |
| DA |
| BC |
=（
| DB |
| CD |
| DC |
| DA |
| BC |
=
| CB |
| DC |
| DA |
| BC |
=
| CD |
| BC |
| DA |
| BC |
=（
| CD |
| DA |
| BC |
=
| CA |
| BC |
故可得
| CA |
| BC |
故选D
点评：本题考查三角形形状的判断，向量的数量积的运算是解决问题的关键，属中档题．
练习册系列答案
相关题目
，
，
，
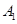是平面直角坐标系中两两不同的四点，若
（λ∈R），
（μ∈R），且,
，则称
是平面直角坐标系中两两不同的四点，若
,
,且
，则称
调和分割
，已知平面上的点
调和分割点
，则下面说法正确的是
，则三角形ABC一定是（ ）