题目内容
用一颗骰子连掷三次，投掷出的数字顺次排成一个三位数，此时：
（1）各位数字互不相同的三位数有多少个？
（2）可以排出多少个不同的数？
（3）恰好有两个相同数字的三位数共有多少个？
（1）各位数字互不相同的三位数有多少个？
（2）可以排出多少个不同的数？
（3）恰好有两个相同数字的三位数共有多少个？
考点：排列、组合及简单计数问题
专题：排列组合
分析：（1）得到一个三位数，分三步进行：先填百位，有6种方法，再填十位，有5种方法，最后填个位，有4种方法，根据分步计数原理可得
（2）分三步进行：先填百位，再填十位，最后填个位，每种都有6种方法，根据分步计数原理可得．
（3）从三个位中任选两个位，填上相同的数字，有6C32 种方法，剩下的一位数字的填法有5种，根据分步计数原理，求出结果．
（2）分三步进行：先填百位，再填十位，最后填个位，每种都有6种方法，根据分步计数原理可得．
（3）从三个位中任选两个位，填上相同的数字，有6C32 种方法，剩下的一位数字的填法有5种，根据分步计数原理，求出结果．
解答：
解：（1）得到一个三位数，分三步进行：先填百位，再填十位，最后填个位．百位上的数字填法有6种，十位上的数字填法有5种，个位上的数字填法有4种，
根据分步计数原理，各位数字互不相同的三位数有6×5×4=120个．
（2）分三步进行：先填百位，再填十位，最后填个位，每种都有6种方法，根据分步计数原理，可以排出6×6×6=216个不同的数．
（3）从三个位中任选两个位，填上相同的数字，有6C32 种方法，剩下的一位数字的填法有5种，根据分步计数原理，恰好有两个相同的数字的三位数有 6C32 C51=90 个．
根据分步计数原理，各位数字互不相同的三位数有6×5×4=120个．
（2）分三步进行：先填百位，再填十位，最后填个位，每种都有6种方法，根据分步计数原理，可以排出6×6×6=216个不同的数．
（3）从三个位中任选两个位，填上相同的数字，有6C32 种方法，剩下的一位数字的填法有5种，根据分步计数原理，恰好有两个相同的数字的三位数有 6C32 C51=90 个．
点评：本题主要考查分步计数原理的应用，正确进行分步并求出每一步的方法数，是解题的关键，属于基础题．
练习册系列答案
相关题目
函数f（x）=
（0≤x≤2π）的值域为（ ）
| sinx-1 | ||
|
| A、[-1，0] | ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
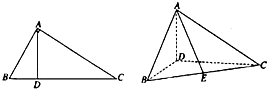如图，在△ABC中，AB⊥AC，AD⊥BC，∠ABC=
已知椭圆C方程：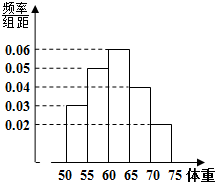
某公司为了了解员工们的健康状况，随机抽取了部分员工作为样本，测量他们的体重（单位：公斤），体重的分组区间为[50，55），[55，60），[60，65），[65，70），[70，75]，由此得到样本的频率分布直方图，如图所示．根据频率分布直方图，估计该公司员工体重的众数是