题目内容
11.用反三角函数值的形式表示下列各式中的x.(1)sinx=-$\frac{1}{4}$,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]
(2)sinx=$\frac{\sqrt{3}}{3}$,x∈[0,π].
分析 由条件利用反正弦函数的定义和性质,求得x的值.
解答 解:(1)∵sinx=-$\frac{1}{4}$,x∈[-$\frac{π}{2}$,$\frac{π}{2}$],∴x=arcsin(-$\frac{1}{4}$)=-arcsin$\frac{1}{4}$.
(2)sinx=$\frac{\sqrt{3}}{3}$,x∈[0,π],∴x=arcsin$\frac{\sqrt{3}}{3}$,或x=π-arcsin$\frac{\sqrt{3}}{3}$.
点评 本题主要考查反正弦函数的定义和性质,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1.函数f(x)=1+2sinxcosx的最小值和周期分别是( )
| A. | 0,π | B. | 1,π | C. | 1,2π | D. | 3,π |
 的焦点为
的焦点为 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 两点.
两点. ,求直线
,求直线 的斜率;
的斜率; 在线段
在线段 上运动,原点
上运动,原点 关于点
关于点 的对称点为
的对称点为 ,求四边形
,求四边形 面积的最小值.
面积的最小值.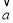 =(1,1),
=(1,1), =(2,5),
=(2,5), =(3,x)满足条件(8
=(3,x)满足条件(8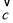 =30,则x=( )
=30,则x=( )