题目内容
2．4名男生和3名女生站成-排．要求男生甲不与女生乙相邻，女生丙不与女生乙相邻，则不同的排法总数为2400．分析 分两类，第一类，若女生乙在两端，第二类，若女生乙不两端，根据分类计数原理可得．
解答 解：第一类，若女生乙在两端，先选1名（除了男生甲和女生丙之外的4人）和女生乙相邻，其他的任意排，故有A21A41A55=960种，
第二类，若女生乙不两端，先选2名（除了男生甲和女生丙之外的4人）排在女生乙的两边与女生乙相邻，把这三人捆绑在一起看做一个复合元素，和另外的4人全排，故有A42A55=1440种，
根据分类计数原理可得，共有960+1440=2400种，
故答案为：2400．
点评 本题主要考查排列与组合及两个基本原理，排列数公式、组合数公式的应用，注意特殊元素和特殊位置要优先排．
练习册系列答案
相关题目
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1，的离心率e=2，若过双曲线右焦点且与渐近线平行的直线与圆x2+y2+4x=8相切，则双曲线的方程为（ ）
| A． | x2-$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
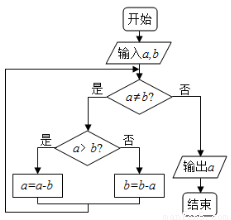
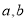分别为8，12，则输出的
（ ）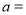