题目内容
10. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,M为PB的中点,平面ADM交PC于N点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,M为PB的中点,平面ADM交PC于N点.(1)求证:PB⊥DN;
(2)求二面角P-DN-A的余弦值.
分析 (1)由题意可得PB⊥MA,DA⊥AB,从而得到DA⊥PA.再由PB⊥DA,得PB⊥平面ADNM,由此能证明PB⊥DN;
(2)以A为坐标原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A-xyz,然后分别求出平面PDN与DNA的一个法向量,由两法向量所成角的余弦值即可求得二面角P-DN-A的余弦值.
解答 (1)证明:∵M为PB的中点,且PA=AB,∴PB⊥MA.
∵∠BAD=90°,∴DA⊥AB.
∵PA⊥底面ABCD,∴DA⊥PA.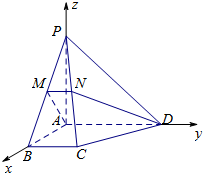
∵PA∩AB=A,∴DA⊥平面PAB,则PB⊥DA.
∵AM∩DA=A,∴PB⊥平面ADNM,
∵DN?平面ADNM,∴PB⊥DN;
(2)解:如图,以A为坐标原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A-xyz.
则A(0,0,0),B(2,0,0),C(2,1,0),D(0,2,0),
P(0,0,2).
由(1)知,PB⊥平面ADNM,∴平面ADNM的法向量为
$\overrightarrow{BP}$=(-2,0,2).
设平面PDN的法向量为$\overrightarrow{n}$=(x,y,z),
∵$\overrightarrow{PC}$=(2,1,-2),$\overrightarrow{PD}$=(0,2,-2),
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PC}=2x+y-2z=0}\\{\overrightarrow{n}•\overrightarrow{PD}=2y-2z=0}\end{array}\right.$,令z=2,则y=2,x=1.
∴$\overrightarrow{n}$=(1,2,2),
∴cos<$\overrightarrow{n},\overrightarrow{BP}$>=$\frac{\overrightarrow{n}•\overrightarrow{BP}}{|\overrightarrow{n}||\overrightarrow{BP}|}$=$\frac{2}{2\sqrt{2}×3}$=$\frac{\sqrt{2}}{6}$.
∴二面角P-DN-A的余弦值为$\frac{\sqrt{2}}{6}$.
点评 本题考查线线平行、线线垂直的证明,考查二面角的余弦值的求法,训练了利用空间向量求解二面角的平面角,是中档题.

 已知定义在R上的函数f(x)及其导函数f′(x)的图象如图所示,则函数y=e-xf(x)的减区间为( )
已知定义在R上的函数f(x)及其导函数f′(x)的图象如图所示,则函数y=e-xf(x)的减区间为( )| A. | (0,1),(4,+∞) | B. | (-∞,1) | C. | (1,+∞) | D. | (-∞,0),(1,4) |
| A. | {5} | B. | {1,3} | C. | {2,6} | D. | {1,3,4,5,6} |