题目内容
已知双曲线实轴在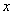 轴,且实轴长为2,离心率
轴,且实轴长为2,离心率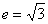 , L是过定点
, L是过定点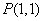 的直线.
的直线.
(1)求双曲线的标准方程;
(2)判断L能否与双曲线交于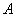 ,
,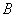 两点,且线段
两点,且线段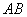 恰好以点
恰好以点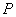 为中点,若存在,求出直线L的方程,若不存,说明理由.
为中点,若存在,求出直线L的方程,若不存,说明理由.
1)∵2a=2 ,∴a=1,又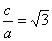 ,∴c=
,∴c=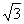 ,∴
,∴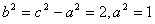 ,
,
∴标准方程为: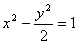 .
.
(2)①:若过点P的直线斜率不存在,则L的方程为: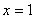 ,
,
此时L与双曲线只有一个交点,不满足题意.
②: 若过点P的直线斜率存在且设为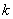 ,则L的方程可设为:
,则L的方程可设为: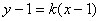 ,
,
设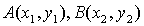 ,AB的中点
,AB的中点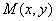 ,
,
由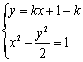 得,
得,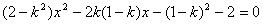 ①
①
显然,要有两个不同的交点,则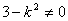 .所以
.所以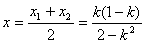 ,要以P为中点,则有
,要以P为中点,则有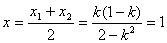 ,解得
,解得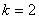 ,当
,当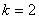 时,方程①为:
时,方程①为: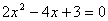 ,该方程无实数根,即L不会与双曲线有交点,
,该方程无实数根,即L不会与双曲线有交点,

练习册系列答案
相关题目
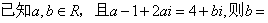
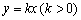 与函数
与函数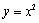 的图象交于点
的图象交于点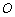 ,
,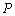 ,过
,过 轴于
轴于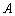 .在
.在 中任取一点,则该点落在阴影部分的概率为________.
中任取一点,则该点落在阴影部分的概率为________.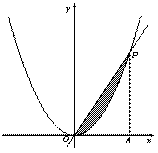
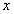
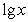
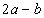
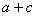
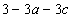
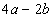
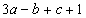
 =
=  、
、 、
、 三个平面上的正投影,则此四棱锥的体积为 ( )
三个平面上的正投影,则此四棱锥的体积为 ( )
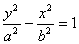 (a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为_____________;
(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为_____________;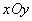 中,离心率为
中,离心率为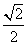 的椭圆
的椭圆
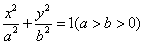 的左顶点为
的左顶点为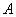 ,过
,过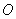 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于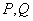 两点,直线
两点,直线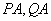 分别与
分别与 轴交于
轴交于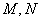 两点.若直线
两点.若直线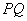 斜率为
斜率为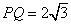 .
.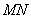 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线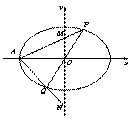
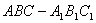 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是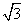 ,D是AC的中点。
,D是AC的中点。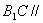 平面
平面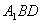 ;
;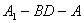 的大小;
的大小;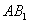 与平面
与平面