题目内容
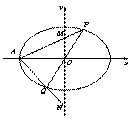
.如图,在平面直角坐标系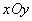 中,离心率为
中,离心率为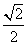 的椭圆
的椭圆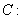
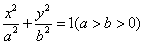 的左顶点为
的左顶点为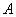 ,过
,过
原点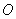 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆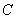 交于
交于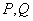 两点,直线
两点,直线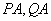 分别与
分别与 轴交于
轴交于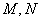 两点.若直线
两点.若直线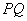 斜率为
斜率为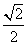 时,
时,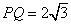 .
.
(1)求椭圆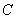 的标准方程; (2)试问以
的标准方程; (2)试问以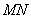 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线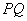 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
解:(1)设 ,
,
∵直线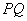 斜率为
斜率为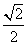 时,
时,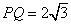 ,∴
,∴ ,∴
,∴
∴ ,∵
,∵ ,∴
,∴ .
.
∴椭圆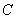 的标准方程为
的标准方程为 .
.
(2)以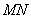 为直径的圆过定点
为直径的圆过定点 .
.
设 ,则
,则 ,且
,且 ,即
,即 ,
,
∵ ,∴直线
,∴直线 方程为:
方程为: ,∴
,∴ ,
,
直线 方程为:
方程为: ,∴
,∴ ,
,
以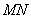 为直径的圆为
为直径的圆为
即 ,
,
∵ ,∴
,∴ ,
,
令 ,
, ,解得
,解得 ,
,
∴以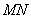 为直径的圆过定点
为直径的圆过定点 .
.

练习册系列答案
相关题目
某企业2014年2月份生产A、B、C三种产品共6000件,根据分层拍样的结果,该企业统计员制作了如下的统计表格:
| 产品类别 | A | B | C |
| 产品数量 | 2600 | ||
| 样本容量 | 260 |
由于不小心,表格中B、C产品的有关数据已被污染看不清楚,统计员记得B产品的样本容量比C产品的样本容量多20,根据以上信息,可得C的产品数量是 ( )
A.160 B.180 C.1600 D.1800
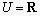 ,集合
,集合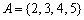 ,
,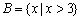 ,则满足
,则满足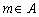 且
且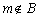 的实数
的实数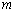 所组成的集合为( )
所组成的集合为( )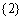 B.
B. C.
C. D.
D.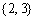
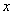 轴,且实轴长为2,离心率
轴,且实轴长为2,离心率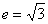 , L是过定点
, L是过定点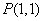 的直线.
的直线.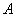 ,
,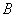 两点,且线段
两点,且线段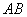 恰好以点
恰好以点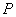 为中点,若存在,求出直线L的方程,若不存,说明理由.
为中点,若存在,求出直线L的方程,若不存,说明理由.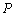 ,且满足
,且满足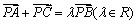 ,则满足条件的
,则满足条件的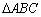 有( )
有( ) 则sin
则sin sin
sin cos
cos cos
cos 等于( )
等于( )  B.
B. C.
C. D.
D.
 则f(x)的值域为( )
则f(x)的值域为( )  B.
B. C.(-2,2) D.
C.(-2,2) D.
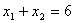
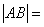 ( )
( )