题目内容
2.已知函数f(x)=log${\;}_{\frac{1}{2}}$(x2-2ax-a)的值域为R,且f(x)在(-2,1-$\sqrt{2}$)上为增函数.则a的取值范围为[0,1].分析 由题意可得,函数y=x2-2ax-a能够取遍所有的正数,由△=4a2+4a≥0,求得a的范围 ①.再根据函数y=x2-2ax-a在(-2,1$-\sqrt{2}$)上是减函数且为正值,得出不等式组求解即可.
解答 解:由函数f(x)=log${\;}_{\frac{1}{2}}$(x2-2ax-a)的值域为R,可得函数y=x2-2ax-a能够取遍所有的正数,
故有△=4a2+4a≥0,求得:a≤-1,或a≥0 ①.
再根据f(x)在(-2,1-$\sqrt{2}$)上是增函数,可得函数y=x2-2ax-a在(-2,1-$\sqrt{2}$)上是减函数且为正值,
故a≥1-$\sqrt{2}$,且当x=1-$\sqrt{2}$时y≥0.
即 a≥1$-\sqrt{2}$,且3$-2\sqrt{2}$-a(3-2$\sqrt{2}$)≥0.
求得:1$-\sqrt{2}$≤a≤1②.
结合①②求得0≤a≤1,
故答案为:[0,1]
点评 本题主要考查复合函数的单调性,对数函数、二次函数的性质,体现了转化的数学思想,属于基础题

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
14.如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )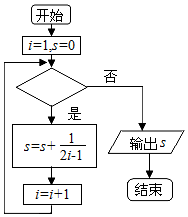

| A. | i≤1008? | B. | i>1008? | C. | i≤1009? | D. | i>1009? |
10.${(x-\frac{1}{{\sqrt{x}}})^6}(2{x^3}+1)$的常数项是( )
| A. | 15 | B. | 17 | C. | -15 | D. | -17 |
14.由曲线y=$\sqrt{x}$,直线y=x所围成的封闭曲线的面积是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
11.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{b}$=6,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |