题目内容
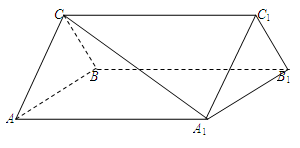
如图,四棱锥P—ABCD中,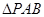 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,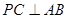 ,E为PD点上一点,满足
,E为PD点上一点,满足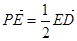
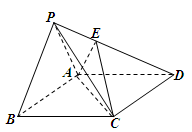
(1)证明:平面ACE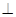 平面ABCD;
平面ABCD;
(2)求直线PD与平面ACE所成角正弦值的大小.
(1) 见解析;(2) .
.
解析试题分析:(1)经过建立空间直角坐标系,求出面 和
和 各自的法向量
各自的法向量 ,通过证明
,通过证明 ,说明面
,说明面
 ;(2)将直线与面所成角的正弦转化为直线所在向量和平面的法向量的夹角的余弦的绝对值求解.
;(2)将直线与面所成角的正弦转化为直线所在向量和平面的法向量的夹角的余弦的绝对值求解.
试题解析:(1)证明:取 的中点
的中点 ,
, ,因为
,因为 ,所以
,所以 ,
,
所以以 为坐标原点建立如图的空间直角坐标系,则
为坐标原点建立如图的空间直角坐标系,则 ,因为
,因为 ,所以
,所以 ,设面
,设面 法向量为
法向量为 ,则
,则 ,令
,令 得
得 ,
, .所以
.所以 ,取面
,取面 法向量为
法向量为 ,因为
,因为 ,所以面
,所以面
 .
.
(2) 解  ,设直线
,设直线 与平面
与平面 所成角大小为
所成角大小为 ,
,
则 .
.
考点:1.空间直角坐标系;2.空间法向量;3.直线与平面所成的角.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
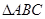 中,
中,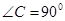 ,
, ,点
,点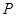 在边
在边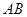 上,设
上,设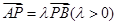 ,过点
,过点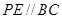 交
交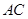 于
于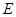 ,作
,作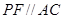 交
交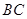 于
于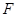 。沿
。沿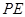 将
将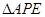 翻折成
翻折成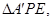 使平面
使平面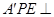 平面
平面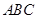 ;沿
;沿 将
将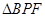 翻折成
翻折成 使平面
使平面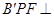 平面
平面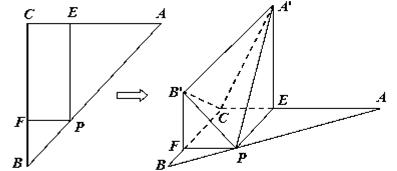
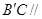 平面
平面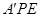 ;
;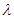 ,使得二面角
,使得二面角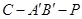 的大小为
的大小为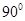 ?若存在,求出
?若存在,求出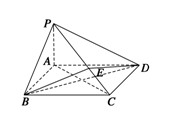
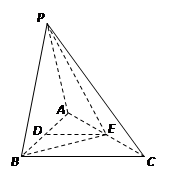
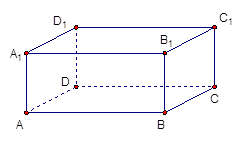
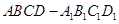 中,
中,
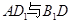 所成角;
所成角;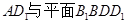 所成角的正弦.
所成角的正弦. ,使得平面
,使得平面
 平面ABD;
平面ABD;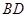 与平面
与平面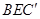 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.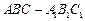 中,
中, ,顶点
,顶点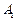 在底面
在底面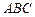 上的射影恰为点
上的射影恰为点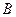 ,且
,且 .
. 平面
平面 ;
; 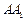 与
与 所成的角的大小;
所成的角的大小;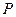 为
为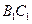 的中点,并求出二面角
的中点,并求出二面角 的平面角的余弦值.
的平面角的余弦值.
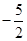 ,1] B.[
,1] B.[  ] D.(-∞,
] D.(-∞,