题目内容
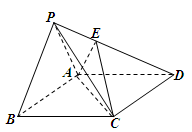
如图,在三棱柱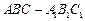 中,
中, ,顶点
,顶点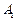 在底面
在底面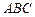 上的射影恰为点
上的射影恰为点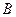 ,且
,且 .
.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)求棱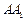 与
与 所成的角的大小;
所成的角的大小;
(Ⅲ)若点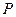 为
为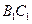 的中点,并求出二面角
的中点,并求出二面角 的平面角的余弦值.
的平面角的余弦值.
证明:(Ⅰ)∵ 面
面 ∴
∴ ,
, 
又 ,
,
∴ 面
面 ,
,
∵ 面
面 , ∴平面
, ∴平面 平面
平面 ;
;
(Ⅱ)以A为原点,建立如图所示的空间直角坐标系,
则 ,
,
 ,
,
 ,
,
故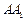 与棱BC所成的角是
与棱BC所成的角是 .
.
(Ⅲ)因为P为棱 的中点,故易求得
的中点,故易求得 .
.
设平面 的法向量为
的法向量为
 ,
,
则 ,由
,由 得
得
令 ,则
,则

而平面 的法向量
的法向量 =(1,0,0),则
=(1,0,0),则
由图可知二面角 为锐角,故二面角
为锐角,故二面角 的平面角的余弦值是
的平面角的余弦值是
解析

练习册系列答案
相关题目
 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).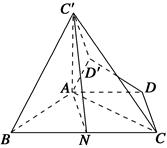
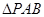 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,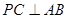 ,E为PD点上一点,满足
,E为PD点上一点,满足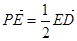
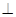 平面ABCD;
平面ABCD;
 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;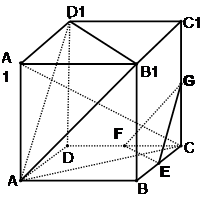
 边长都为2,且
边长都为2,且
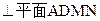 ,
, 的中点,
的中点,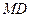
 。(2分)
。(2分) 的距离。(5分)
的距离。(5分)
 -
- 中,
中, 分别为
分别为 的中点. 应用空间向量方法求 解下列问题.
的中点. 应用空间向量方法求 解下列问题. 
 平面
平面 ;
;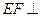 平面
平面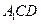 .
.
