题目内容
6．如图，在矩形ABCO中，阴影部分的面积为2．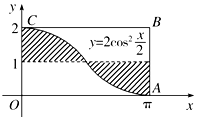
分析 由题意，S=2${∫}_{0}^{\frac{π}{2}}（2co{s}^{2}\frac{x}{2}-1）$dx，即可得出结论．
解答 解：由题意，S=2${∫}_{0}^{\frac{π}{2}}（2co{s}^{2}\frac{x}{2}-1）$dx=2$sinx{|}_{0}^{\frac{π}{2}}$=2，
故答案为2．
点评 本题考查利用定积分求面积，考查学生的计算能力，比较基础．
练习册系列答案
提分百分百检测卷系列答案
相关题目
18．已知f（x）是定义域为R的奇函数，当x＜0时，f（x）=x2-x，那么当x＞0时f（x）的解析式是（ ）
| A． | f（x）=-x2-x | B． | f（x）=x2+x | C． | f（x）=x2-x | D． | f（x）=-x2+x |
17．设E，F分别为平行四边形ABCD中AB，AD的中点，$\overrightarrow{EC}$+$\overrightarrow{FC}$=（ ）
| A． | $\frac{1}{2}$$\overrightarrow{AC}$ | B． | $\overrightarrow{AC}$ | C． | $\frac{3}{2}$$\overrightarrow{AC}$ | D． | 2$\overrightarrow{AC}$ |
14．函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$的定义域为（ ）
| A． | $（-\frac{1}{2}，\frac{3}{4}）$ | B． | $[{-\frac{1}{2}，\frac{3}{4}}]$ | C． | $（-∞，\frac{1}{2}]$ | D． | $（-\frac{1}{2}，0）∪（0，+∞）$ |
15．△ABC的内角A，B满足cosAcosB＞sinAsinB，则△ABC是（ ）
| A． | 锐角三角形 | B． | 钝角三角形 | C． | 直角三角形 | D． | 等边三角形 |
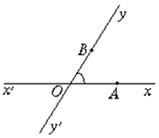如图，有两条相交成60°角的直线xx′，yy′，交点是O，甲、乙分别在Ox，Oy上，起初甲离O点3km，乙离O点1km，后来两人同时用每小时4km的速度，甲沿xx′方向，乙沿y′y方向步行，问：