Question

16．已知三棱柱ABC-A₁B₁C₁的各棱长都为1，M是底面上BC边的中点，N是侧棱CC₁上的点，且CN=$\frac{1}{4}$CC₁，求证：AB₁⊥MN．

Answer 1

分析 设AB中点为O，作OO₁∥AA₁，以O为原点，OB为x轴，OC为y轴，OO₁为z轴，建立空间直角坐标系，利用向量法能证明AB₁⊥MN．

解答 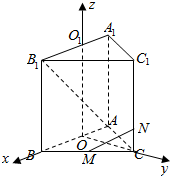解：设AB中点为O，作OO₁∥AA₁，
以O为原点，OB为x轴，OC为y轴，OO₁为z轴，建立空间直角坐标系，
由已知得A（-$\frac{1}{2}$，0，0），B₁（$\frac{1}{2}，0，1$），
B（$\frac{1}{2}，0，0$），C（0，$\frac{\sqrt{3}}{2}$，0），C₁（0，$\frac{\sqrt{3}}{2}$，1），
M（$\frac{1}{4}$，$\frac{\sqrt{3}}{4}$，0），N（0，$\frac{\sqrt{3}}{2}$，$\frac{1}{4}$），
$\overrightarrow{A{B}_{1}}$=（1，0，1），$\overrightarrow{MN}$=（-$\frac{1}{4}$，$\frac{\sqrt{3}}{4}$，$\frac{1}{4}$），
$\overrightarrow{A{B}_{1}}•\overrightarrow{MN}$=-$\frac{1}{4}+0+\frac{1}{4}$=0，
∴AB₁⊥MN．

点评 本题考查异面直线垂直的证明，是中档题，解题时要认真审题，注意向量法的合理运用．