Question

12．已知函数f（x）满足f（x+1）=f（x-1），且f（x）是偶函数，当x∈[0，1]时，f（x）=x，若在区间[-1.3]上函数g（x）=f（x）-kx-k有4个零点，求实数k的取值范围．

Answer 1

分析 根据f（x+1）=f（x-1），可得f（x）是周期为2的周期函数． 再由f（x）是偶函数，当x∈[0，1]时，f（x）=x，可得函数在[-1，3]上的解析式．根据题意可得函数y=f（x）的图象与直线y=kx+k 有4个交点，数形结合可得实数k的取值范围．

解答 解：∵函数f（x）满足f（x+1）=f（x-1），
故有f（x+2）=f（x），
故f（x）是周期为2的周期函数．
再由f（x）是偶函数，当x∈[0，1]时，f（x）=x，
由于函数g（x）=f（x）-kx-k有4个零点，故函数y=f（x）的图象与直线y=kx+k 有4个交点，如图所示：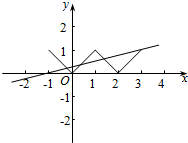

把点（3，1）代入y=kx+k，可得k=$\frac{1}{4}$，
数形结合可得实数k的取值范围是 （0，$\frac{1}{4}$]，

点评 本题主要考查函数的周期性的应用，函数的零点与方程的根的关系，体现了转化、数形结合的数学思想，属于中档题．