题目内容
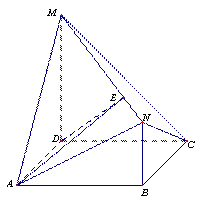
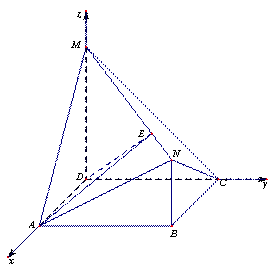
如图,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB∥MD,且NB=1,MD=2;(Ⅰ)求证:AM∥平面BCN;
(Ⅱ)求AN与平面MNC所成角的正弦值;
(Ⅲ)E为直线MN上一点,且平面ADE⊥平面MNC,求 的值.
的值.
解:(Ⅰ)∵ABCD是正方形,
∴BC∥AD.
∵BCË平面AMD,AD 平面AMD,
平面AMD,
∴BC∥平面AMD.
∵NB∥MD,
∵NBË平面AMD,MD 平面AMD,
平面AMD,
∴NB∥平面AMD.
∵NB BC=B,NB
BC=B,NB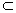 平面BCN, BC
平面BCN, BC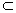 平面BCN,
平面BCN,
∴平面AMD∥平面BCN
∵AM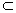 平面AMD,
平面AMD,
∴AM∥平面BCN
(也可建立直角坐标系,证明AM垂直平面BCN的法向量,酌情给分)
(Ⅱ)
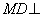 平面ABCD,ABCD是正方形,所以,可选点D为原点,DA,DC,DM所在直线分别为x,y,z轴,建立空间直角坐标系(如图)
平面ABCD,ABCD是正方形,所以,可选点D为原点,DA,DC,DM所在直线分别为x,y,z轴,建立空间直角坐标系(如图)
 则
则 ,
, ,
, ,
,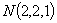 .
.

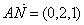 ,
,
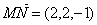 ,
,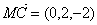 ,
,
设平面MNC的法向量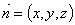 ,
,
则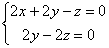 ,令
,令 ,则
,则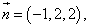
设AN与平面MNC所成角为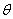 ,
,

 . ……9分
. ……9分
(Ⅲ)设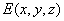 ,
,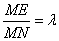 ,
,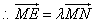 ,
,
又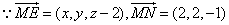 ,
,
 E点的坐标为
E点的坐标为 ,
,
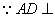 面MDC,
面MDC,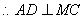 ,
,
欲使平面ADE⊥平面MNC,只要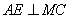 ,
,
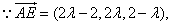
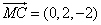 ,
,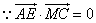
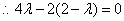 ,
,
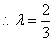

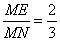 .
.

练习册系列答案
相关题目
 轴上的椭圆
轴上的椭圆 过点
过点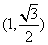 ,离心率为
,离心率为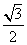 ,点
,点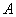 为其右顶点.过点
为其右顶点.过点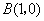 作直线
作直线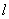 与椭圆
与椭圆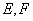 两点,直线
两点,直线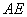 ,
, 与直线
与直线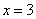 分别交于点
分别交于点 ,
,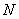 .
.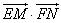 的取值范围.
的取值范围. 按任意顺序组成的没有重复数字的数组,记为
按任意顺序组成的没有重复数字的数组,记为 ,设
,设 ,其中
,其中 .
. ,求
,求 的值;
的值; ;
; ,
, 都成立.)
都成立.) 满足约束条件
满足约束条件 ,则
,则 的最大值是
的最大值是 (B)
(B)  (C) 1 (D)
(C) 1 (D) 
 ,则⊙O的半径为 ;
,则⊙O的半径为 ; .
.
 的值是
的值是 (C)
(C) (D)
(D)
 ,
, ,
, ,数列
,数列 的前n项和为
的前n项和为 ,则n= .
,则n= . 的展开式中
的展开式中 的系数是 .
的系数是 .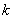 组中抽取其号码的个位数与
组中抽取其号码的个位数与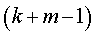 的个位数相同的个体,其中
的个位数相同的个体,其中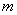 是第1组随机抽取的号码的个位数,则当
是第1组随机抽取的号码的个位数,则当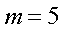 时,从第7组中抽取的号码是( )
时,从第7组中抽取的号码是( )