题目内容
已知中心在原点,焦点在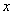 轴上的椭圆
轴上的椭圆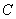 过点
过点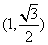 ,离心率为
,离心率为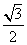 ,点
,点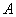 为其右顶点.过点
为其右顶点.过点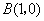 作直线
作直线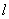 与椭圆
与椭圆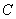 相交于
相交于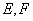 两点,直线
两点,直线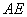 ,
, 与直线
与直线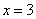 分别交于点
分别交于点 ,
,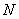 .
.
(Ⅰ)求椭圆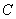 的方程;
的方程;
(Ⅱ)求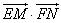 的取值范围.
的取值范围.
解:(Ⅰ)设椭圆的方程为 ,
,
依题意得 解得
解得 ,
, .
.
所以椭圆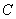 的方程为
的方程为 .
.
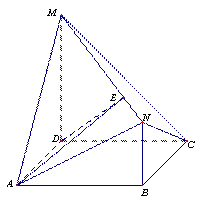
(Ⅱ)显然点 .
.
(1)当直线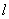 的斜率不存在时,不妨设点
的斜率不存在时,不妨设点 在
在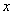 轴上方,易得
轴上方,易得 ,
, ,所以
,所以 .
.
(2)当直线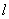 的斜率存在时,由题意可设直线
的斜率存在时,由题意可设直线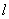 的方程为
的方程为 ,显然
,显然 时,不符合题意.
时,不符合题意.
由 得
得 .
.
设 ,则
,则 .
.
直线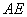 ,
, 的方程分别为:
的方程分别为: ,
,
令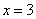 ,则
,则 .
.
所以 ,
, .
.
所以





 .
.
因为 ,所以
,所以 ,所以
,所以 ,即
,即 .
.
综上所述,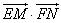 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
 的不等式
的不等式 无解,则实数
无解,则实数 的取值范围为 .
的取值范围为 .  与曲线
与曲线 有且仅有一个公共点,则
有且仅有一个公共点,则
 (
( >
> )的焦点为
)的焦点为 ,已知点
,已知点 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足 .过弦
.过弦 的中点
的中点 作抛物线准线的垂线
作抛物线准线的垂线 ,垂足为
,垂足为 ,则
,则 的最大值为
的最大值为 B. 1 C.
B. 1 C.  D. 2
D. 2 中,已知点
中,已知点 (
(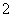 ≤
≤ )上的一个动点,点
)上的一个动点,点 的延长线上.当
的延长线上.当 时,则点
时,则点 :
: ,
, ;命题
;命题 :
: ,
, .
. 是假命题 B.
是假命题 B. 是真命题 D.
是真命题 D. 是真命题
是真命题 中,
中, ,则
,则 ,若
,若 为等差数列,且
为等差数列,且 ,则数列
,则数列 .若
.若 ,使
,使 ,则称
,则称 为函数
为函数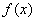 的一个“生成点”.函数
的一个“生成点”.函数 的值.
的值.