题目内容
已知锐角三角形ABC中,向量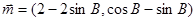 ,
,

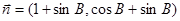 ,且
,且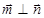 。
。
(1)求角B的大小;
(2)当函数y=2sin2A+cos(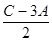 )取最大值时,判断三角形ABC的形状。
)取最大值时,判断三角形ABC的形状。
(1) ;(2)三角形
;(2)三角形 是正三角形.
是正三角形.
解析试题分析:(1)由 可得:
可得: ,整理化简得:
,整理化简得:
即 ,又
,又 为锐角三角形,
为锐角三角形,
 ;(2)由(1)
;(2)由(1) ,所以
,所以 ,这样,可将
,这样,可将 中的角C换掉,只留角A,将其看作关于角A的函数,利用三角函数即可求得其最大值时角A值,这样根据三个角的大小可确定三角形的形状.
中的角C换掉,只留角A,将其看作关于角A的函数,利用三角函数即可求得其最大值时角A值,这样根据三个角的大小可确定三角形的形状.
试题解析:
 ,
,
 2分
2分
即 ,
,
即 ,
, 4分
4分
又 锐角三角形
锐角三角形 中,
中,
 6分
6分
(2)由(1)知 ,所以
,所以
=
=

 9分
9分
当 时,即
时,即 时
时 有最大值.
有最大值.
此时 ,
, 三角形
三角形 是正三角形. 12分
是正三角形. 12分
考点:1、向量与三角函数;2、三角函数的最值及三角形的形状.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
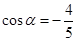 ,
,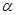 为第三象限角.
为第三象限角.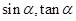 的值;(2)求
的值;(2)求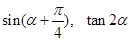 的值.
的值.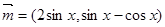 ,
, ,函数
,函数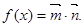
 的解析式;
的解析式; 中,角
中,角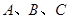 的对边为
的对边为 ,若
,若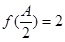 ,
,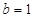 ,
,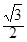 ,求a的值.
,求a的值.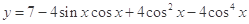 的最大值与最小值.
的最大值与最小值.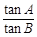 =
=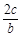 .
.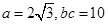 ,求
,求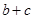 的值。
的值。 ,求下列各式的值:
,求下列各式的值: ;
; .
. ,且
,且 ,求
,求 的值;
的值; 为第二象限角,且
为第二象限角,且 ,求
,求 的值.
的值. ,试求式子
,试求式子 的值.
的值.  ,点P,Q分别是在角A的两边上不同于点A的动点.
,点P,Q分别是在角A的两边上不同于点A的动点.
 ,求AQ的长;
,求AQ的长; ,求sin(2α+β)的值.
,求sin(2α+β)的值.