题目内容
已知tan( )=2,θ为锐角,求cos(
)=2,θ为锐角,求cos( +θ)的值.
+θ)的值.
解:∵tan2( )=tan(
)=tan(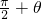 )=-cotθ,
)=-cotθ,
又tan2( )=
)= =
= =-
=- ,
,
∴cotθ= ∴tanθ=
∴tanθ= .…(6分)
.…(6分)
∵θ为锐角∴sinθ= ,cosθ=
,cosθ= ,…(8分)
,…(8分)
∴cos( +θ)=cos
+θ)=cos cosθ-sin
cosθ-sin sinθ
sinθ
=
=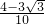 .…(12分)
.…(12分)
分析:通过二倍角的正切公式以及诱导公式,求出sinθ,cosθ,利用两角和的余弦函数求出表达式的值.
点评:本题考查两角和与差的三角函数,同角三角函数的基本关系式,考查计算能力.
 )=tan(
)=tan(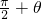 )=-cotθ,
)=-cotθ,又tan2(
 )=
)= =
= =-
=- ,
,∴cotθ=
 ∴tanθ=
∴tanθ= .…(6分)
.…(6分)∵θ为锐角∴sinθ=
 ,cosθ=
,cosθ= ,…(8分)
,…(8分)∴cos(
 +θ)=cos
+θ)=cos cosθ-sin
cosθ-sin sinθ
sinθ=

=
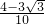 .…(12分)
.…(12分)分析:通过二倍角的正切公式以及诱导公式,求出sinθ,cosθ,利用两角和的余弦函数求出表达式的值.
点评:本题考查两角和与差的三角函数,同角三角函数的基本关系式,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目