题目内容
6．参数方程$\left\{\begin{array}{l}{x=co{s}^{2}θ}\\{y=sinθ}\end{array}\right.$（θ为参数）所表示的曲线为（ ）| A． | 抛物线的一部分 | B． | 一条抛物线 | C． | 双曲线的一部分 | D． | 一条双曲线 |
分析 参数方程$\left\{\begin{array}{l}{x=co{s}^{2}θ}\\{y=sinθ}\end{array}\right.$（θ为参数），消去参数化为：y2+x=1，即y2=1-x，x∈[0，1]．即可判断出结论．
解答 解：参数方程$\left\{\begin{array}{l}{x=co{s}^{2}θ}\\{y=sinθ}\end{array}\right.$（θ为参数），消去参数化为：y2+x=1，即y2=1-x，x∈[0，1]．
∴表示的曲线是抛物线的一部分，
故选：A．
点评 本题考查了参数方程化为普通方程、三角函数基本关系式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
中考解读考点精练系列答案
相关题目
17．若曲线y=ex+ax+b在点（0，2）处的切线l与直线x+3y+1=0垂直，则a+b=（ ）
| A． | -3 | B． | 3 | C． | 1 | D． | -1 |
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）．
如图，AD是△ABC的高，AE是△ABC的外接圆的直径，点B和点C在直线AE的两侧．求证：AB•AC=AD•AE．
16．如图，在△ABC中，$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{NC}$，P是BN上的一点，若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}$，则实数m的值为（ ）
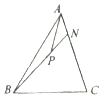
| A． | $\frac{9}{11}$ | B． | $\frac{2}{11}$ | C． | $\frac{3}{11}$ | D． | $\frac{1}{11}$ |