题目内容
已知定点A(0,2),B(0,-2),C(2,0),动点P满足:
•
=m|
|2
(I)求动点P的轨迹方程,并说明方程表示的曲线类型;
(II)当m=2时,设点P(x,y)(y≥0),求
的取值范围.
| AP |
| BP |
| pc |
(I)求动点P的轨迹方程,并说明方程表示的曲线类型;
(II)当m=2时,设点P(x,y)(y≥0),求
| y |
| x-8 |
(Ⅰ)设动点的坐标为P(x,y),则
=(x,y-2),
=(x,y+2),
=(2-x,-y)
∵
•
=m|
|2,
∴(x,y-2)•(x,y+2)=m(
)2
∴x2+y2-4=m[(x-2)2+y2]
即(1-m)x2+(1-m)y2+4mx-4m-4=0,
若m=1,则方程为x=2,表示过点(2,0)且平行于y轴的直线;
若m≠1,则方程化为:(x-
)2+y2=(
)2,表示以(
,0)为圆心,以
为半径的圆;
(Ⅱ)当m=2时,方程化为(x-4)2+y2=4;
设
=k,则y=kx-8k,圆心(4,0)到直线y=kx-8k的距离d=
=2时,
解得k=±
,又y≥0,所以点P(x,y)所在图形为上半个圆(包括与x轴的两个交点),
故直线与半圆相切时k=-
;
当直线过x轴上的两个交点时知k=0;
因此
的取值范围是[-
,0].
| AP |
| BP |
| PC |
∵
| AP |
| BP |
| PC |
∴(x,y-2)•(x,y+2)=m(
| (2-x)2+(-y)2 |
∴x2+y2-4=m[(x-2)2+y2]
即(1-m)x2+(1-m)y2+4mx-4m-4=0,
若m=1,则方程为x=2,表示过点(2,0)且平行于y轴的直线;
若m≠1,则方程化为:(x-
| 2m |
| m-1 |
| 2 |
| m-1 |
| 2m |
| m-1 |
| 2 |
| |1-m| |
(Ⅱ)当m=2时,方程化为(x-4)2+y2=4;
设
| y |
| x-8 |
| |4k-8k| | ||
|
解得k=±
| ||
| 3 |
故直线与半圆相切时k=-
| ||
| 3 |
当直线过x轴上的两个交点时知k=0;
因此
| y |
| 8-x |
| ||
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
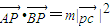
 的取值范围.
的取值范围.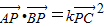
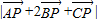 的最大值和最小值.
的最大值和最小值.