题目内容
已知定点A(0,2),B(0,-2),C(2,0),动点P满足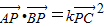
(1)求动点P的轨迹方程,并说明方程表示的曲线
(2)当k=2时,求
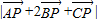 的最大值和最小值.
的最大值和最小值.
【答案】分析:(1)将向量用坐标进行表示,利用动点P满足 ,可得动点P的轨迹方程,进而分类说明方程表示的曲线;
,可得动点P的轨迹方程,进而分类说明方程表示的曲线;
(2)当k=2时,轨迹为圆,进而可知 表示点(x,y)到点
表示点(x,y)到点 的距离,故可求.
的距离,故可求.
解答:解:(1)设动点P的坐标为(x,y), ,
,
 ,
,
由已知x2+y2-4=k[(x-2)2+y2]
∴(k-1)x2+(k-1)y2-4kx+4(k+1)=0…(3)分
①∴当k=1时,x=2方程表示一条直线 …(4)分
②当k≠1时,
∴
∴k≠1时,方程表示圆心为 的圆 …(6)分
的圆 …(6)分
(2)k=2点p的方程为(x-4)2+y2=4

 …(8)分
…(8)分
 表示点(x,y)到点
表示点(x,y)到点 的距离 …(10)分
的距离 …(10)分
圆心(4,0)到 的距离为
的距离为
∴ 的最小值为
的最小值为 ,
,
最大值为 …(13)分
…(13)分
点评:本题以向量为载体,考查轨迹问题,关键是用坐标表示向量,正确理解代数式的几何意义是解题的关键.
 ,可得动点P的轨迹方程,进而分类说明方程表示的曲线;
,可得动点P的轨迹方程,进而分类说明方程表示的曲线;(2)当k=2时,轨迹为圆,进而可知
 表示点(x,y)到点
表示点(x,y)到点 的距离,故可求.
的距离,故可求.解答:解:(1)设动点P的坐标为(x,y),
 ,
,
 ,
,由已知x2+y2-4=k[(x-2)2+y2]
∴(k-1)x2+(k-1)y2-4kx+4(k+1)=0…(3)分
①∴当k=1时,x=2方程表示一条直线 …(4)分
②当k≠1时,

∴

∴k≠1时,方程表示圆心为
 的圆 …(6)分
的圆 …(6)分(2)k=2点p的方程为(x-4)2+y2=4

 …(8)分
…(8)分 表示点(x,y)到点
表示点(x,y)到点 的距离 …(10)分
的距离 …(10)分圆心(4,0)到
 的距离为
的距离为
∴
 的最小值为
的最小值为 ,
,最大值为
 …(13)分
…(13)分点评:本题以向量为载体,考查轨迹问题,关键是用坐标表示向量,正确理解代数式的几何意义是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
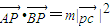
 的取值范围.
的取值范围.