Question

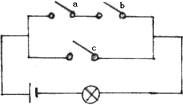
如图，在开关电路中，开关k₁，k₂，k₃开或关的概率都为，且是相互独立的，则灯亮的概率是    ．

Answer 1

【答案】分析：每个开关的闭合情况都有2种，故所有的情况共有2³种，而满足灯亮的情况有2²+1=5种，由此求得灯亮的概率．
解答：解：每个开关的闭合情况都有2种，故所有的情况共有2³=8种，
而满足灯亮的情况有2²+1=5种，故灯亮的概率为 ，
故答案为 ．
点评：本题主要考查相互独立事件的概率、以及古典概率的计算公式的应用，属于中档题．