题目内容
在R上定义运算⊙:x⊙y=
,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )
| x |
| 2-y |
分析:要解的不等式即
>0,解得a<x<a+1.再由不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,可得
,哟此解得实数a的范围.
| x-a |
| 2-(x+1-a) |
|
解答:解:关于x的不等式(x-a)⊙(x+1-a)>0 即
>0,即
<0,解得a<x<a+1.
再由不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,
可得
,解得-2≤a≤1,
故选C.
| x-a |
| 2-(x+1-a) |
| x-a |
| x-(a+1) |
再由不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,
可得
|
故选C.
点评:本题主要考查新定义,分式不等式的解法,题体现了等价转化的数学思想,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 :x
:x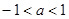 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.