题目内容
18.已知等差数列{an}的前n项和为Sn,a4=10,S4=28,数列$\left\{{\frac{1}{{{S_n}+2}}}\right\}$的前n项和为Tn,则T2017=$\frac{2017}{4038}$.分析 利用已知条件求出等差数列的前n项和,化简所求的通项公式,然后求和即可.
解答 解:等差数列{an}的前n项和为Sn,a4=10,S4=28,可得a1+a4=14,解得a1=4,10=4+3d,解得d=2,
Sn=4n+$\frac{n(n-1)}{2}×2$=n2+3n,
$\frac{1}{{S}_{n}+2}$=$\frac{1}{{n}^{2}+3n+2}$=$\frac{1}{n+1}-\frac{1}{n+2}$,
Tn=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n+1}-\frac{1}{n+2}$=$\frac{1}{2}-\frac{1}{n+2}$,
则T2017=$\frac{1}{2}-\frac{1}{2019}$=$\frac{2017}{4038}$.
故答案为:$\frac{2017}{4038}$.
点评 本题考查数列求和,等差数列通项公式以及性质的应用,考查计算能力.

练习册系列答案
相关题目
8.已知A(-1,0),B(3,2),C(0,-2),则过这三点的圆方程为( )
| A. | (x-$\frac{3}{2}$)2+y2=25 | B. | (x+$\frac{3}{2}$)2+y2=$\frac{1}{4}$ | C. | (x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$ | D. | x2+(y-$\frac{3}{2}$)2=$\frac{5}{2}$ |
10.设F为抛物线C:y2=2px的焦点,过F且倾斜角为60°的直线交曲线C于A,B两点(B点在第一象限,A点在第四象限),O为坐标原点,过A作C的准线的垂线,垂足为M,则|OB|与|OM|的比为3.
7.已知α为第二象限角,sin(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,则tanα的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $-\frac{4}{3}$ | D. | -3 |
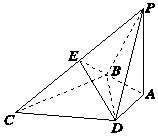 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC. 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.