题目内容
3.设向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,3).(Ⅰ)若(3$\overrightarrow{a}$+2$\overrightarrow{b}$)∥(-$\overrightarrow{a}$+λ$\overrightarrow{b}$),求实数λ的值;
(Ⅱ)若(2$\overrightarrow{a}$-$\overrightarrow{b}$)⊥(k$\overrightarrow{a}$+$\overrightarrow{b}$),求实数k的值.
分析 (Ⅰ)根据平面向量的坐标运算与共线定理,列出方程求出λ的值;
(Ⅱ)根据平面向量的坐标运算与互相垂直的数量积为0,列出方程求出k的值.
解答 解:(Ⅰ)∵向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,3),
∴3$\overrightarrow{a}$+2$\overrightarrow{b}$=(4,9),
-$\overrightarrow{a}$+λ$\overrightarrow{b}$=(-2-λ,3λ-1),
又(3$\overrightarrow{a}$+2$\overrightarrow{b}$)∥(-$\overrightarrow{a}$+λ$\overrightarrow{b}$),
∴4(3λ-1)-9(-2-λ)=0,
解得λ=-$\frac{2}{3}$;
(Ⅱ)∵2$\overrightarrow{a}$-$\overrightarrow{b}$=(5,-1),
k$\overrightarrow{a}$+$\overrightarrow{b}$=(2k-1,k+3),
且(2$\overrightarrow{a}$-$\overrightarrow{b}$)⊥(k$\overrightarrow{a}$+$\overrightarrow{b}$),
∴5(2k-1)-(k+3)=0,
解得k=$\frac{8}{9}$.
点评 本题考查了平面向量的坐标运算与向量的共线和垂直的应用问题,是基础题目.

练习册系列答案
相关题目
14.对变量x,y有观测数据(xi,yi)(i=1,2,3,4,5),得表1;对变量u,v有观测数据(ui,vi)(i=1,2,3,4,5),得表2.由这两个表可以判断( )
表1:
表2:
表1:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
| u | 1 | 2 | 3 | 4 | 5 |
| v | 25 | 20 | 21 | 15 | 13 |
| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y负相关,u与v正相关 | ||
| C. | 变量x与y负相关,u与v负相关 | D. | 变量x与y正相关,u与v负相关 |
11.为了得到函数y=cos(2x-$\frac{2π}{3}$),x∈R的图象,只要把函数y=cos2x,x∈R的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |
12.某商店每天以每瓶5元的价格从奶厂购进若干瓶24小时新鲜牛奶,然后以每瓶8元的价格出售,如果当天该牛奶卖不完,则剩下的牛奶就不再出售,由奶厂以每瓶2元的价格回收处理.
(1)若商场一天购进20瓶牛奶,求当天的利润y(单位:元)关于当天需求量n(单位:瓶,n∈N)的函数解析式;(2)商店记录了50天该牛奶的日需求量(单位:瓶),整理得下表:
假设商店一天购进20瓶牛奶,以50天记录的各需求量的频率作为各需求量发生概率,求当天利润低于60元的概率.
(1)若商场一天购进20瓶牛奶,求当天的利润y(单位:元)关于当天需求量n(单位:瓶,n∈N)的函数解析式;(2)商店记录了50天该牛奶的日需求量(单位:瓶),整理得下表:
| 日需求量n(瓶) | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数 | 5 | 5 | 8 | 12 | 10 | 6 | 4 |
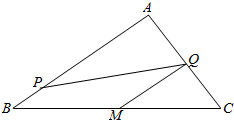 如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.
如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.