题目内容
(本小题满分12分)已知椭圆: 上任意一点到两焦点
上任意一点到两焦点 距离之和为
距离之和为 ,离心率为
,离心率为 ,动点
,动点 在直线
在直线 上,过
上,过 作直线
作直线 的垂线
的垂线 ,设
,设 交椭圆于
交椭圆于 点.
点.
(1)求椭圆 的标准方程;
的标准方程;
(2)证明:直线 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(1) ,(2)
,(2)
【解析】
试题分析:由椭圆定义,椭圆上任意一点到两焦点距离之和为常数
 ,得
,得 ,离心率
,离心率 ,于是
,于是 ,求出椭圆的标准方程;第二步是定点定值问题,动点
,求出椭圆的标准方程;第二步是定点定值问题,动点 在直线
在直线 上,可设
上,可设 ,
, ,写出向量
,写出向量 和
和 的坐标,利用
的坐标,利用 ,得出
,得出
 ……②,最后找出
……②,最后找出 和
和 的斜率,由于
的斜率,由于 ……①,因为
……①,因为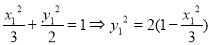 ;又因为②得:
;又因为②得: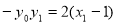 代入①得
代入①得

试题解析:(1)由条件得: ,解得:
,解得: ,
,
所以椭圆 :
:
(2)设
 ,所以:
,所以: ,即:
,即:
 ……①
……①
又因为: …….②,且
…….②,且 …….③,把①③代入②
…….③,把①③代入②
化简得:
考点:1.待定系数法求椭圆的标准方程;2.平面向量的数量积;3.减元化简;
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
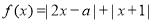 .
.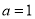 时,解不等式
时,解不等式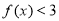 ;
;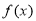 的最小值为1,求a的值.
的最小值为1,求a的值. ,则
,则 ( )
( ) B.
B. C.
C. 或0 D.
或0 D. 的定义域为 .
的定义域为 . 为虚数单位,复数
为虚数单位,复数
 的虚部
的虚部 记作
记作
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 中,已知
中,已知 ,
, ,且
,且 是
是 的个位数字,
的个位数字, 是
是 的前
的前 项和,则
项和,则 .
. 的图象上各点的横坐标伸长到原来的3倍(纵坐标不变),再向右平移
的图象上各点的横坐标伸长到原来的3倍(纵坐标不变),再向右平移 个单位,所得函数图像的一个对称中心是( )
个单位,所得函数图像的一个对称中心是( ) B.
B. C.
C. D.
D.
 ,则实数
,则实数 的取值范围为 .
的取值范围为 . 是
是 的高,
的高, 是
是 外接圆的直径,若
外接圆的直径,若 ,则
,则 .
.