题目内容
已知二次函数

(1)当 时,
时,
 的最大值为
的最大值为 ,求
,求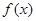 的最小值;
的最小值;
(2)对于任意的 ,总有
,总有 ,试求
,试求 的取值范围.
的取值范围.


(1)当
 时,
时,
 的最大值为
的最大值为 ,求
,求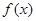 的最小值;
的最小值;(2)对于任意的
 ,总有
,总有 ,试求
,试求 的取值范围.
的取值范围.(1)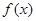 的最小值为
的最小值为 (2)
(2)
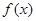 的最小值为
的最小值为 (2)
(2)
试题分析:(1)由已知条件可知,当
 时
时 取得最大值,由此得到
取得最大值,由此得到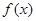 的解析式,进而得到f(x)的最小值.
的解析式,进而得到f(x)的最小值.(2)根据已知条件结合换元法把命题转化为:任给
 ,不等式
,不等式 ,恒成立.由此入手,能够求出实数a的取值范围.
,恒成立.由此入手,能够求出实数a的取值范围.试题解析:(1)由
 知
知 ,故当
,故当 时
时 取得最大值
取得最大值 ,即
,即 ,所以
,所以 ,所以
,所以 ,所以
,所以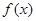 的最小值为
的最小值为 .
.(2)对于任意的
 ,总有
,总有 ,令
,令 ,
,则命题转化为:任给
 ,不等式
,不等式 ,
,当
 时,
时, 满足
满足 ;
;当
 时,有
时,有 对于任意的
对于任意的 恒成立;
恒成立;由
 得
得 ,所以
,所以 ,
,所以要使
 恒成立,则有
恒成立,则有 .
.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 (
( 为实数,
为实数, ),
), ,⑴若
,⑴若 ,且函数
,且函数 的值域为
的值域为 ,求
,求 的表达式;
的表达式; ,且函数
,且函数 .
. (a≠0)满足
(a≠0)满足 ,
, 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数 的一个零点.又
的一个零点.又 (
( >0).
>0).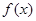 的解析式;
的解析式; 在
在 上有解,求实数
上有解,求实数 ,求
,求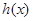 的单调区间.
的单调区间.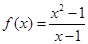 ,
,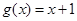 ;②
;②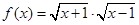 ,
,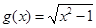 ;③
;③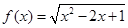 ,
,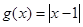 ;④
;④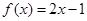 ,
,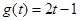 .其中表示同一个函数的有( ).
.其中表示同一个函数的有( ).
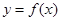 (
(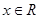 )的图象如图所示,则不等式
)的图象如图所示,则不等式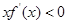 的解集为________.
的解集为________.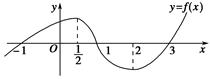
 的零点,则[x0]等于________.
的零点,则[x0]等于________.